Lösung von Aufgabe 13.2P (SoSe 22)
Aus Geometrie-Wiki
Version vom 18. Juli 2022, 08:59 Uhr von Matze2000 (Diskussion | Beiträge)
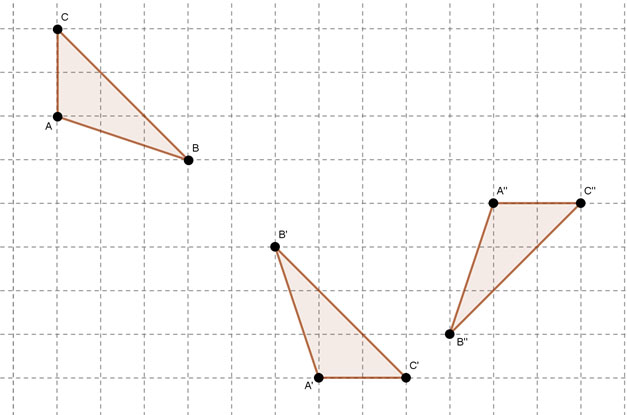
Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen 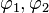 , mit
, mit 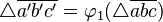 und
und 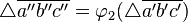 .
.
- wie heißen die beiden Abbildungen
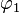 und
und 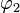 ?
?
- Zeichnen Sie jeweils für
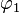 und
und 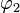 die passende Anzahl von Spiegelachsen in die Skizze ein.
die passende Anzahl von Spiegelachsen in die Skizze ein.
- Durch welche Ersatzabbildung kann die Verkettung
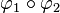 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze ein.