Verkettung zweier Geradenspiegelungen WS 22 23

Verkettung von Abbildungen

Definition IX.1 : (Verkettung von Abbildungen)

Unter einer Verkettung von Abbildungen versteht man das Hintereinanderausführen zweier oder mehrerer Abbildungen $\varphi _{1}..\varphi _{n}$.
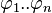Schreibweise: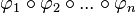 $\varphi _{1}\circ\varphi _{2}\circ ... \circ \varphi _{n}$.

Anmerkung: In der Literatur wird die Reihenfolge der Verkettung unterschiedlich angewendet: 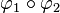$\varphi _{1}\circ\varphi _{2}$ kann bedeuten, dass man zuerst 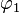$\varphi _{1}$ und dann 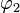$\varphi _{2}$ ausführen muss, aber auch die umgekehrte Reihenfolge wird verwendet. Wir einigen uns im Rahmen dieser Veranstaltung für die erste Variante, also die Ausführungsreihenfolge von links nach rechts.

Verkettung zweier Geradenspiegelungen

Gegeben seien zwei Geraden a und b. Wir betrachten die Verkettung $S_{a}\circ S_{b}$.
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der beiden Geraden a und b gibt es? Ihre Antwort:

Wir betrachten zunächst zwei sich schneidende Spiegelgeraden: Experimentieren Sie mit dem nachfolgenden Applet, indem Sie die Verkettung der beiden Geradenspiegelungen ausführen, d. h. auf das Dreieck anwenden. Welche Zusammenhänge entdecken Sie?

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

Satz IX.1 :

Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Jeder Punkt P liegt dabei mit seinem Bildpunkt $P''=S_{a}\circ S_{b}(P)$ auf einem Kreis k um S.
Beweis:

Satz IX.2 :

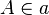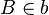Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten $A\in a$ und $B\in b$, die von S jeweils verschieden sind. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Für einen beliebigen Punkt P und seinen Bildpunkt $P''=S_{a}\circ S_{b}(P)$ gilt: $\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|$.
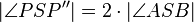Beweis:

Eine Abbildung, wie wir sie auf dieser Seite kennengelernt haben, nennen wir auch Drehung. Definieren Sie im Folgenden den Begriff Drehung:

Definition IX.2 (Drehung):

...

Die Punktspiegelung als Sonderfall der Drehung

Definition IX.3 (Punktspiegelung):

Eine Punktspiegelung ist eine Abbildung, die bei der Verkettung zweier senkrecht aufeinanderstehender Spiegelgeraden entsteht.

Die Punktspiegelung ist damit eine Drehung mit einem Drehwinkel, der das Maß 180 hat und wird deshalb auch als Halbdrehung bezeichnet.
Experimentieren Sie mit dem folgenden GeoGebra-Applet. Vergleichen Sie dabei die beiden Möglichkeiten: Spiegle Objekt an Gerade und Spiegle Objekt an Punkt.
Können Sie besondere Eigenschaften der Punktspiegelung entdecken, die die allgemeine Drehung nicht aufweist?
Bewegen Sie den Punkt A. Was fällt Ihnen auf?

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

Satz IX.3 :

Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 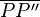$\overline{PP''}$, mit $P''=S_{a}\circ S_{b}(P)$.
Beweis: Übungsaufgabe

Satz IX.4 :

Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.
Beweis: Übungsaufgabe

Satz IX.5 :

Bei einer Punktspiegelung 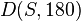$D(S,180)$ wird eine Gerade g für die gilt: 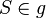$S\in g$ stets auf sich selbst abgebildet.
Beweis:

Mit Hilfe der Sätze zur Punktspiegelung lassen sich einige wichtige Winkelsätze der Geometrie beweisen:

Satz IX.6 :

Paare von Scheitelwinkeln sind zueinander kongruent.
Beweis:

Satz IX.7 (Wechselwinkelsatz) :

Wechselwinkel an geschnittenen Parallelen sind kongruent zueinander.
Beweis:

Satz IX.8 (Stufenwinkelsatz) :

Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander.
Beweis:


Anmerkung: Bei den Beweisen zum Wechselwinkel- bzw. Stufenwinkelsatz gehen wir davon aus, dass es durch einen beliebigen Punkt P außerhalb einer Geraden g immer genau eine Parallele h zu g gibt, die durch den Punkt P verläuft. Dass es in der ebenen Geometrie eine solche Parallele geben muss können wir beweisen, dass es höchstens eine solche Parallele gibt wird durch ein Axiom festgelegt. Es handelt sich hier um das berühmte Parallelenaxiom. Näheres hierzu finden Sie im Sekundarstufen-Wiki!

Verkettung zweier Geradenspiegelungen mit zueinander parallelen Achsen

Wir betrachten nun zwei parallele Spiegelgeraden: Experimentieren Sie mit dem nachfolgenden Applet, indem Sie die Verkettung der beiden Geradenspiegelungen ausführen, d. h. auf das Dreieck anwenden. Welche Zusammenhänge entdecken Sie?

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

Satz IX.9 :

Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Jeder Punkt P hat dabei zu seinem Bildpunkt $P''=S_{a}\circ S_{b}(P)$ einen Abstand der doppelt so groß ist als der Abstand der beiden Spiegelgeraden.
Beweis:
Obige Abbildung nennt man auch Translation, Parallelverschiebung oder einfach nur Verschiebung. Definieren Sie den Begriff Translation formal korrekt:

Definition IX.4 (Translation):

...