Lösung von Aufgabe 10.2P (WS 23 24)
Aus Geometrie-Wiki
Version vom 13. Januar 2024, 15:04 Uhr von Matze2000 (Diskussion | Beiträge)
Beweisen Sie Satz IX.2:
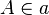 und
und 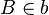 , die von S jeweils verschieden sind. Wir betrachten die Verkettung
, die von S jeweils verschieden sind. Wir betrachten die Verkettung  . Für einen beliebigen Punkt P und seinen Bildpunkt
. Für einen beliebigen Punkt P und seinen Bildpunkt  gilt:
gilt: 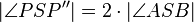 .
.--Capricorn (Diskussion) 21:32, 9. Jan. 2024 (CET)
Super! Der Beweis ist weitestgehend korrekt. Das ist schon echt gut :) Hier noch ein paar kleine Anmerkungen:
1. Vergiss nicht die Betragsstriche zu setzen, wenn du über die Größe eines Winkel sprichst.
2. 3) kannst du noch mit "Satz der Winkeladdition" begründen.
3. Bei 4) fehl noch |<PSP´´|=
4. In die Voraussetzung müssen noch die Informationen über die Spiegelungen also welche Geraden gibt es, wie werden diese verkettet, an welchem Punkt schneiden sie sich und welche Punkte gehören zu den Geraden :) --Matze2000 (Diskussion) 14:55, 13. Jan. 2024 (CET)


