Lösung von Aufgabe 2.1
Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Lösungsvorschlag
Wenn eine Gerade g senkrecht auf der Strecke s steht und durch den Mittelpunkt der Strecke verläuft, dann ist g Mittelsenkrechte der Strecke s.
Das ist korrekt!--Schnirch 10:50, 3. Nov. 2010 (UTC)
Wenn alle Punkte einer Punktmenge m zu den Endpunkten der Strecke den gleichen Abstand haben, dann ist die Punktmenge die Mittelsenkrechte der Strecke. Bin aber nicht sicher, ob das sauber definiert ist?--Sommer80 09:38, 24. Okt. 2010 (UTC)
Nach Ihrer Definition könnte ich eine Punktmenge nehmen, die z. B. nur aus einem Punkt besteht,
der zu den Endpunkten einer Strecke den gleichen Abstand hat. Das wären dann alle
Punkte Ihrer Punktmenge. Dieser eine Punkt ist aber sicherlich nicht die
Mittelsenkrechte. Korrekt müsste es heißen: Wenn eine Punktmenge alle Punkte enthält,
die zu den Endpunkten einer Strecke jeweils den gleichen Abstand haben, dann ist die Punktmenge
Mittelsenkrechte der Strecke.
Ist Ihnen der Unterschied klar?--Schnirch 10:50, 3. Nov. 2010 (UTC)
Du hast eine Strecke AB
A ------------------------- B
:
:
: jeder dieser Punkte hat für sich, wenn ich das jetzt richtig eingezeichnet habe,
den selben Abstand zu Punkt A und zu Punkt B
Wenn die Menge aller Punkte zu den Endpunkten der Strecke AB den gleichen Abstand haben, dann bilden sie die Mittelsenkrechte. <-- das wäre mein Vorschlag.
@sommer80: Müsstest du nicht voraussetzen, dass der Begriff "senkrecht" bereits bekannt ist?
Wir setzen voraus, dass der Begriff senkrecht bereits definiert ist!--Schnirch 10:50, 3. Nov. 2010 (UTC)
Die Definition von Sommer80 ist richtig. Die Mittelsenkrechte einer Strecke AB wird über den Abstand alles Punkte definiert die ein und denselben Abstand zu den A und B haben. So werden alle anderen Punkte ausgeschlossen und man erhält die Mittelsenkrechtengerade. Den Der Mittepunkt wird ja auch über den Abstand definiert. AM = MB 25.10.2010
Die Definition von Sommer80 ist nicht richtig, siehe Anmerkungen oben--Schnirch 10:50, 3. Nov. 2010 (UTC)
Wenn eine Gerade g die Strecke  in zwei kongruente Teilstrecken
in zwei kongruente Teilstrecken 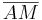 und
und 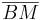 teilt, dann ist g die Mittelsenkrechte von
teilt, dann ist g die Mittelsenkrechte von  , wenn für einen beliebigen Punkt P auf der Geraden g gilt, dass
, wenn für einen beliebigen Punkt P auf der Geraden g gilt, dass 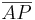 =
=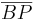 .--Jbo-sax 14:33, 1. Nov. 2010 (UTC)
.--Jbo-sax 14:33, 1. Nov. 2010 (UTC)

