Lösung von Aufg. 7.3
Aus Geometrie-Wiki
Version vom 23. November 2010, 15:53 Uhr von Schnirch (Diskussion | Beiträge)
Satz:
- Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
- Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
- Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
- Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
Beweis
- Es seien
 und
und 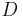 drei Punkte, die nicht komplanar sind.
drei Punkte, die nicht komplanar sind.
- Es seien
zu zeigen
- ...
Annahme:
- Es gibt drei der Punkte vier Punkte
 , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
- Es gibt drei der Punkte vier Punkte

