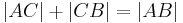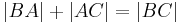11
Aus Geometrie-Wiki
Version vom 23. November 2010, 16:16 Uhr von Engel82 (Diskussion | Beiträge)
Inhaltsverzeichnis |
Axiome
Hier geht es zu den Definitionen WS10/11
Hier geht es zu den Sätze WS10/11
- Inzidenzaxiome:
AXIOM I/0
- Geraden sind Punktmengen.
AXIOM I/1 (Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
- weitere Bezeichnungsmöglichkeit von Geraden
- Eine Gerade g, die durch zwei verschiedene Punkte A und B eindeutig bestimmt ist wird auch mit AB bezeichnet.
AXIOM I/2
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
AXIOM I/3
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Axiom I/4
- Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
Axiom I/5
- Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Axiom I/6
- Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
Axiom I/7
- Es gibt vier Punkte, die nicht komplanar sind.
- Abstandsaxiome:
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
 und
und  gibt es eine eindeutig bestimmte nicht negative reelle Zahl
gibt es eine eindeutig bestimmte nicht negative reelle Zahl 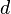 mit
mit 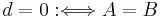 .
.
Axiom II.2:
- Für zwei beliebige Punkte
 und
und  gilt
gilt 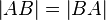 .
.
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 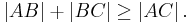
- Für drei beliebige Punkte
- Falls
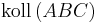 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Falls
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear.
kollinear.