Lösung von Aufg. 7.8
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Gegeben sei ein Kreis k und ein Mittelpunkt M.
Eine Strecke  ist dann eine Sehne des Kreises k, wenn
ist dann eine Sehne des Kreises k, wenn 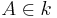 und
und 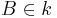
korrekt--Schnirch 14:02, 9. Dez. 2010 (UTC)
Eine Strecke  ist dann ein Durchmesser des Kreises k, wenn
ist dann ein Durchmesser des Kreises k, wenn 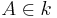 ,
, 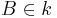 und durch den Mittelpunkt M geht.
und durch den Mittelpunkt M geht.
im letzten Teil fehlt noch was: ... und die Streckedurch den Mittelpunkt M verläuft.--Schnirch 14:02, 9. Dez. 2010 (UTC)
- Eine Strecke
 ist dann ein Kreisdurchmesser, wenn die Sehne durch den Mittelpunkt M des Kreises k geht.* --Halikarnaz 11:13, 11. Dez. 2010 (UTC)
ist dann ein Kreisdurchmesser, wenn die Sehne durch den Mittelpunkt M des Kreises k geht.* --Halikarnaz 11:13, 11. Dez. 2010 (UTC)
Eine Strecke 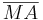 ist dann ein Radius des Kreises k, wenn
ist dann ein Radius des Kreises k, wenn 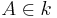 --Engel82 17:26, 23. Nov. 2010 (UTC)
--Engel82 17:26, 23. Nov. 2010 (UTC)
das ist korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)
Sehne: Wenn A und B zu dem Kreis k gehören, wird die Strecke  Kreissehne genannt.
Kreissehne genannt.
... Kreissehne des Kreises k genannt.--Schnirch 14:02, 9. Dez. 2010 (UTC)
Durchmesser:
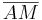 +
+  =
=  , wenn A und B Element k sind und M der Mittelpunkt des Kreises k ist.
, wenn A und B Element k sind und M der Mittelpunkt des Kreises k ist.
korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)
Radius:Eine Strecke 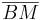 heißt dann Kreisradius, wenn der Punkt B auf dem Kreis k liegt und M der Mittelpunkt ist.
--Snoopy 1 14:29, 1. Dez. 2010 (UTC)
heißt dann Kreisradius, wenn der Punkt B auf dem Kreis k liegt und M der Mittelpunkt ist.
--Snoopy 1 14:29, 1. Dez. 2010 (UTC)
korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)

