Lösung von Aufg. 10.3

Formulieren Sie den Beweis von Satz VI.1, ohne das Tabellenbeweischema zu verwenden. Ferner mögen Sie angehalten sein, die mathematische Formelsprache zu vermeiden. Kurz und gut, ein Beweis mit eigenen Worten, grammatikalisch korrekt formuliert.

Gegeben sei eine Strecke $\overline{AB}$. Es gibt genau einen Mittelpunkt M der Strecke $\overline{AB}$, wobei der Abstand von M zu A und M zu B gleich ist (Def. Mittelpunkt)
Es sei ein Punkt Q, der nicht auf der Geraden $\ AB$ liegt. In der Halbebene AB,Q+ gibt es ein Punkt P, der in dieser Halbebene liegt. Es entsteht der Winkel PMB mit dem Maß 90 (Def. rechter Winkel).
Die Gerade 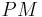$\ PM$ ist die Mittelsenkrechte von $\overline{AB}$. (Def. Relation senkrecht+ Def. Mittelsenkrechte).--Engel82 16:02, 15. Dez. 2010 (UTC)