Lösung von Aufg. 7.1
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Vor: g, P ist nicht Element g
Beh: Es existiert genau eine Ebene E, g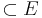 ,
, 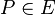
1) 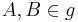 _____Axiom I/1
_____Axiom I/1
2) nkoll(A,P,B)_______________laut Vor und 1)
3) zu drei nkoll(A,P,B)________Axiom I/4 und 2)
gibt es genau eine Ebene E
4)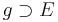 _________Axiom I/5
_________Axiom I/5
5) Behauptung stimmt
Die Eindeutigkeit das genau eine Ebene E existiert, lässt sich auf das Axiom I/4 zurückführen
--Engel82 17:11, 23. Nov. 2010 (UTC)
Die Lösung von Engel82 ist korrekt, prima!--Schnirch 13:40, 9. Dez. 2010 (UTC)
Warum ist g Obermenge von E? Müsste es in Punkt 4) nicht entweder 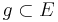 oder
oder 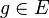 heißen? --Studentxyz 12:38, 16. Jan. 2011 (UTC)
heißen? --Studentxyz 12:38, 16. Jan. 2011 (UTC)
Lösungsvorschlag 2
vielen Dank für dieses gescannte Bild. Schritt 2 können Sie weglassen und den ersten Teil in Schritt 4 auch,
ansonsten ist alles korrekt!--Schnirch 13:40, 9. Dez. 2010 (UTC)
-----------------------------------------------------------------------------------------------
Lösungsvorschlag 3:
Voraussetzung:Es sei eine Gerade g und ein Punkt P, 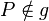
 sei die Menge aller Ebenen.
sei die Menge aller Ebenen.
Behauptung: 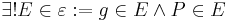
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 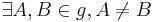
|
Axiom I.2 |
| (II) | nkoll(A,B,P) | I, Vor. (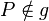 ), Def I.2 (kollinear) ), Def I.2 (kollinear)
|
| (III) | 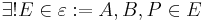
|
II, Axiom I.4 |
| (IV) | 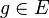
|
I, III, Axiom I.5 |
| (V) | 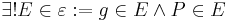
|
III, IV |
qed.
--Studentxyz 13:25, 16. Jan. 2011 (UTC)

