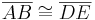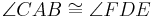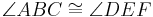11
Hier geht es zu den Axiome WS10/11
Hier geht es zu den Definitionen WS10/11
Inhaltsverzeichnis |
Sätze
Sätze I
Satz I.1
Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Satz I.2 (Kontraposition von Satz I.1)
Es seien g und h zwei Geraden. Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Satz I.3 (Existenz von drei Geraden)
Es existieren mindestens drei paarweise verschiedene Geraden.
Satz I.4
(?)
Satz I.5
Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Satz I.6
Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Satz I.7
Jede Ebene enthält (wenigstens) drei Punkte.
Sätze II
Satz II.1
Aus  folgt
folgt 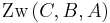 .
.
Satz II.2
Aus  folgt
folgt  .
.
Satz II.3
Es sei  mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt  oder
oder 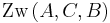 oder
oder 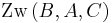 .
.
Satz II.4
Es sei 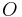 ein Punkt einer Geraden
ein Punkt einer Geraden  .
.
Die Teilmengen 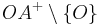 ,
, 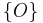 und
und 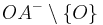 bilden eine Klasseneinteilung der Geraden
bilden eine Klasseneinteilung der Geraden  .
.
Sätze III
Satz III.1 (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
Jede Strecke hat genau einen Mittelpunkt.
Sätze IV
Satz IV.1
Wenn 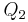 ein Punkt der Halbebene
ein Punkt der Halbebene 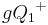 ist, dann gilt
ist, dann gilt 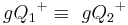 und
und  .
.
Satz IV.2
Halbebenen sind konvexe Punktmengen
Satz IV.3
Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Sätze V
Satz V.1
Das Innere eines Winkels ist konvex.
Satz V.2
Wenn der Punkt  im Inneren des Winkels
im Inneren des Winkels  und nicht auf einem der Schenkel des Winkels
und nicht auf einem der Schenkel des Winkels  liegt, dann ist die Größe der beiden Teilwinkel
liegt, dann ist die Größe der beiden Teilwinkel 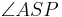 und
und 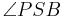 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels  .
.
Satz V.3 (Existenz von rechten Winkeln)
Es gibt rechte Winkel.
Satz V.4
Jeder rechte Winkel hat das Maß 90.
Satz V.5 (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)
Es sei  eine Gerade der Ebene
eine Gerade der Ebene  . Ferner sei
. Ferner sei  ein Punkt auf
ein Punkt auf  . In der Ebene
. In der Ebene  gibt es genau eine Gerade
gibt es genau eine Gerade 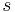 , die durch
, die durch  geht und senkrecht auf
geht und senkrecht auf  steht.
steht.
Sätze VI
Satz VI.1 (Existenz und Eindeutigkeit der Mittelsenkrechten)
Jede Strecke hat in jeder Ebene, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
Satz VI.1 1/2
Es sei 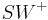 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt
. Dann gilt 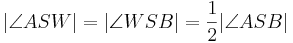 .
.
Satz VI.2 (Existenz und Eindeutigkeit der Winkelhalbierenden)
Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Sätze VII
Satz VII.1
Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.
Satz VII.2
Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.
Satz VII.3
Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.
Satz VII.4 (Kongruenzsatz WSW)
Wenn für zwei Dreiecke  und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
gelten,
dann sind die beiden Dreiecke  und
und  kongruent zueinander.
kongruent zueinander.
Der Kongruenzsatz SSS
Hier dürfen und sollen Sie sich austoben. Für den Beweis des Kongruenzsatzes SSS werden Sie sinnvollerweise den Basiswinkelsatz benötigen. Weil dieser jedoch von so zentraler Bedeutung ist, haben wir ihm einen eigenen Unterpunkt auf der Hauptseite spendiert. Sie dürfen ihn also hier vorab als wahr voraussetzen.
Satz VII.5 Basiswinkelsatz
In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Satz VII.6 (Mittelsenkrechtenkriterium)
Eine Menge  von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 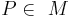 gilt:
gilt: 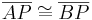 .
.
Satz VII.6a
Wenn ein Punkt  zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von
 gehört.)
gehört.)
Satz VII.6b
Wenn ein Punkt  zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von
 gehört)
gehört)
Sätze VIII
Satz VIII.1 (schwacher Außenwinkelsatz)
Die Größe eines jeden Außenwinkels eines Dreiecks ist jeweils größer als die Größe eines jeden Innenwinkels dieses Dreiecks, der kein Nebenwinkel zu dem gewählten Außenwinkel des Dreiecks ist.
Lemma 2
Wenn ein Punkt  im Inneren des Winkels
im Inneren des Winkels  liegt, dann liegt der gesamte Strahl
liegt, dann liegt der gesamte Strahl 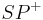 im Inneren des Winkels
im Inneren des Winkels  .
.
Korollar 1 zum schwachen Außenwinkelsatz
In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Korollar 2 zum schwachen Außenwinkelsatz
Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Sätze IX
Satz IX.1 (Existenz und Eindeutigkeit des Lotes)
Zu jedem Punkt  außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
Satz IX.2 (Der größeren Seite liegt der größere Winkel gegenüber)
Es sei  ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
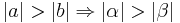
Satz IX.3 (Dem größeren Winkel liegt die größere Seite gegenüber)
Es sei  ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
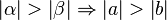
Sätze X
Satz X.1 (Umkehrung des Stufenwinkelsatzes)
Es seien  und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von  mit
mit  und
und  entstehen mögen.
entstehen mögen.
Wenn die beiden Stufenwinkel  und
und  kongruent zueinander sind, dann sind die Geraden
kongruent zueinander sind, dann sind die Geraden  und
und  parallel zueinander.
parallel zueinander.
Sätze XI
Satz XI.1 (Existenz von Parallelen)
Zu jedem Punkt  außerhalb einer Geraden
außerhalb einer Geraden  gibt es eine Gerade
gibt es eine Gerade  , die durch
, die durch  geht und parallel zu
geht und parallel zu  ist.
ist.
Sätze XII
Satz XII.1 (Stufenwinkelsatz)
Es seien  und
und  zwei zueinander parallele Geraden, die durch eine dritte Gerade
zwei zueinander parallele Geraden, die durch eine dritte Gerade  geschnitten werden. Die bei diesem Schnitt entstehenden Stufenwinkel sind kongruent zueinander.
geschnitten werden. Die bei diesem Schnitt entstehenden Stufenwinkel sind kongruent zueinander.
Satz XII.2 (Wechselwinkelsatz)
Es seien  und
und  zwei zueinander parallele Geraden, die durch eine dritte Gerade
zwei zueinander parallele Geraden, die durch eine dritte Gerade  geschnitten werden. Die bei diesem Schnitt entstehenden Wechselwinkel sind kongruent zueinander.
geschnitten werden. Die bei diesem Schnitt entstehenden Wechselwinkel sind kongruent zueinander.
Satz XII.3
Es seien  und
und  zwei zueinander parallele Geraden, die durch eine dritte Gerade
zwei zueinander parallele Geraden, die durch eine dritte Gerade  geschnitten werden. Die bei diesem Schnitt entstehenden entgegengesetzt liegenden Winkel sind supplementär zueinander.
geschnitten werden. Die bei diesem Schnitt entstehenden entgegengesetzt liegenden Winkel sind supplementär zueinander.