Lösung von Aufg. 13.5
Aus Geometrie-Wiki
Version vom 25. Januar 2011, 19:02 Uhr von Engel82 (Diskussion | Beiträge)
Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt. Dieser Punkt ist der Mittelpunkt des Umkreises des Dreiecks.
Vor: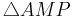
Beh: mab,mbc,mac schneiden sich in einem Punkt P
1) Für alle Punkte X der mab der Seite  gilt:____________Mittelsenkrechtenkriterium
gilt:____________Mittelsenkrechtenkriterium
|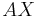 |=|
|=|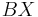 |
|
2)Für alle Punkte X der mac der Seite  gilt:____________Mittelsenkrechtenkriterium
gilt:____________Mittelsenkrechtenkriterium
|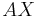 |=|
|=|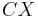 |
|
3) Für den Schnittpunkt P der mab und mac gilt:____________________________2), 3)
|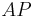 |= |
|= |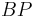 |=|
|=|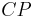 |
|
4)|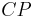 |=|
|=|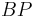 |_____________________Mittelsenkrechtenkriterium
|_____________________Mittelsenkrechtenkriterium
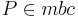
5) P ist der Schnittpunkt der drei Mittelsenkrechten_________________3),4)
mab, mbc,mac. --Engel82 18:00, 25. Jan. 2011 (UTC)

