Aufgabe Kontinuum 01 WS 10 11
Aus Geometrie-Wiki
Version vom 31. Januar 2011, 10:01 Uhr von Shaun15 (Diskussion | Beiträge)
Mark behauptet:
- Zu jedem Winkel α mit 0≤ α<2
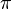 gibt es genau einen Punkt B auf dem Kreis.
gibt es genau einen Punkt B auf dem Kreis.
- Zu jedem Punkt B gibt es genau eine Tangente an den Kreis.
- Jede Tangente schneidet die x Achse in genau einem Punkt A.
- Es gibt genau so viele reelle Zahlen α mit 0≤ α<2
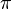 wie Punkte auf der x-Achse.
wie Punkte auf der x-Achse.
Man kommentiere die "Beweisführung" von Mark.

