Lösung von Aufg. 13.3

Man beweise: Ein Punkt $\ P$ gehört genau dann zur Winkelhalbierenden des Winkels $\ \alpha$, wenn er zu den Schenkeln von $\ \alpha$ jeweils denselben Abstand hat.

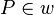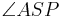
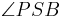
Vor: $P \in w$, , $\angle ASP$ $\cong$$\angle PSB$
Beh: P hat sowohl zum Strahl p als auch zum Strahl q ein und denselben Abstand.
( $\overline {AP}$ $\cong$$\overline {BP}$ )

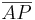
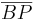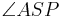
1)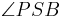$\angle ASP$ $\cong$$\angle PSB$ __________________Vor
2) Lote werden durch P auf die jeweiligen Schenkel des Winkels________________Existenz und Eindeutigkeit des Lotes
$\angle ASB$ gefällt
. A und B sind Lotfußpunkte. 3)|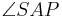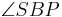$\angle {SAP}$| =|$\angle {SBP}$| =90________________2)
4)$\overline {SP}$= $\overline {SP}$___________________trivial
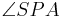
5)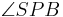$\angle SPA$$\cong$$\angle SPB$__________________1), 2) und Innenwinkelsumme im Dreieck
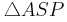
6)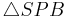$\triangle {ASP}$ $\cong$$\triangle {SPB}$______________WSW,1), 4),5)
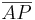
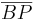7) $\overline {AP}$$\cong$ $\overline {BP}$______________________6)--Engel82 17:22, 25. Jan. 2011 (UTC)

Vor P hat sowohl zum Strahl p als auch zum Strahl q ein und denselben Abstand.
( $\overline {AP}$ $\cong$$\overline {BP}$ )
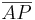
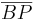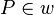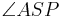
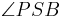
Beh: $P \in w$, $\angle ASP$ $\cong$$\angle PSB$

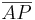
1)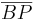$\overline {AP}$$\cong$ $\overline {BP}$___________________Vor.
2) Lote werden durch P auf die jeweiligen Schenkel des Winkels________________Existenz und Eindeutigkeit des Lotes
$\angle ASB$ gefällt
. A und B sind Lotfußpunkte. 3)|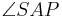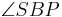$\angle {SAP}$| =|$\angle {SBP}$| =90_________________2)
4)$\overline {SP}$$\cong$ $\overline {SP}$___________________trivial
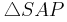
5)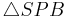$\triangle {SAP}$ $\cong$$\triangle {SPB}$__________________SsW, 1),3),4),Korollar 1 und Satz:der größeren Seite liegt der größere Winkel gegenüber.
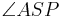
6)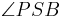$\angle ASP$ $\cong$$\angle PSB$_________________________5)
7)SP+ ist Winkelhalbierende ____________________6)
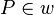$P \in w$--Engel82 17:33, 25. Jan. 2011 (UTC)

• • • • • • • • • • • Muss das bei Schritt 5 nicht Dreieck SAP und Dreieck SPB heißen ????! **********************

Stimmt. Danke--Engel82 09:02, 27. Jan. 2011 (UTC)

• • • • • • • • • • • • Kannst du die Punkte A und B verwenden um die Winkel zu beschreiben und alles wenn du sie erst in Schritt 2 als Lotfußpunkte festlegst?--Einfach ich 10:47, 2. Feb. 2011 (UTC)

Wenn man es ganz genau nimmt, müsste man in die Behauptung folgendes schreiben: P hat sowohl zum Strahl p als auch zum Strahl q ein und denselben Abstand. Und in Schritt zwei werden dann die Lotfußpunkte festgelegt. Aber man kann sich ja auf die Skizze berufen. --Engel82 09:59, 3. Feb. 2011 (UTC)

ja, passen Sie auf, dass die Punkte, die Sie verwenden auch nach Voraussetzung da sind oder vorab
 konstruiert werden, ansonsten ist der Beweis in Ordnung!--Schnirch 13:49, 4. Feb. 2011 (UTC)