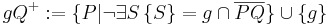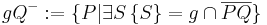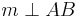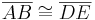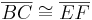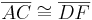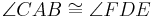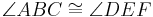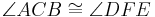11
Hier geht es zu den Axiome WS10/11
Hier geht es zu den Sätze WS10/11
Definitionen (1)
Definition: (n-stellige Relation)
Es seien 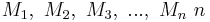 Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus
Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 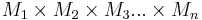 ist eine
ist eine 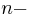 stellige Relation.
stellige Relation.
Definition: (Klasseneinteilung eine Menge)
Es sei  eine Menge und
eine Menge und 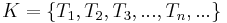 eine Menge von Teilmengen von
eine Menge von Teilmengen von  .
.
 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  , wenn
, wenn
- notwendige Bedingung 1: Keine der Teilmengen ist die leere Menge.
- notwendige Bedingung 2: Je zwei Teilmengen sind disjunkt.
- notwendige Bedingung 3: Die Vereinigung aller Teilmengen ergibt wieder die Menge
 .
.
Mengen sind disjukt, wenn die Schnittmenge dieser Mengen die leere Menge ist, bzw. die Mengen keine gemeinsamen Objekte besitzen.
Definitionen (2)
Definitionen I
Definition I/2 (kollinear)
Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
Schreibweise kolinear: koll(A, B, C, ...)
Schreibweise nicht kollinear: nkoll(A, B, C)
Definition I/3 (Inzidenz Punkt Ebene)
Ein Punkt P inzidiert mit einer Ebene E, wenn P ein Element der Ebene E ist.
Definition I/4 (Inzidenz Gerade Ebene)
Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört.
Definition I/5 (Raum)
Die Menge aller Punkte P wird Raum genannt.
Definition I/6 (komplanar)
Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält.
Schreibweise: komp(A, B, C, D, ...)
analoge Schreibweise: nkomp(A, B, C, D, ...) für nicht komplanar
Definition I/7 (komplanar für Geraden)==
Zwei Geraden g und h sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen.
Schreibweise: komp(g, h)
Definition I/8 (Geradenparallelität)
Zwei Geraden g und h sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind.
In Zeichen: g || h.
Definition I/9 (windschief)
Zwei Geraden g und h sind windschief, wenn sie schnittpunktfrei und nicht parallel sind.
Definition I/10 (parallel für Ebenen)
Zwei Ebene E1 und E2 sind parallel, wenn sie keinen Punkt gemeinsam haben.
Definitionen II
Definition II.1 (Abstand)
Der Abstand zweier Punkte  und
und  ist die Zahl, die nach dem Abstandsaxiom den Punkten
ist die Zahl, die nach dem Abstandsaxiom den Punkten  und
und  zugeordnet werden kann.
zugeordnet werden kann.
Schreibweise: 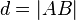 .
.
Definition II.2 (Zwischenrelation)
Ein Punkt  liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn
, wenn  gilt und der Punkt
gilt und der Punkt  sowohl von
sowohl von  als auch von
als auch von  verschieden ist.
verschieden ist.
Schreibweise: 
Definition II.3 (Strecke, Endpunkte einer Strecke)
Es seien  und
und  zwei verschiedene Punkte. Die Punktmenge, die
zwei verschiedene Punkte. Die Punktmenge, die  und
und  sowie alle Punkte, die zwischen
sowie alle Punkte, die zwischen  und
und  liegen, enthält, heißt Strecke
liegen, enthält, heißt Strecke  .
.
- Wieso zwei verschiedene Punkte? Laut meinen Kenntnissen stimmt diese Definition so nicht!
Definition II.4 (Länge einer Strecke)
Es seien  und
und  zwei verschiedene Punkte. Der Abstand
zwei verschiedene Punkte. Der Abstand 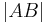 heißt Länge der Strecke
heißt Länge der Strecke  .
.
Definition II.5 (Halbgerade, bzw. Strahl)
Halbgerade 
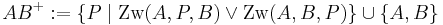
Halbgerade 
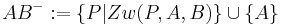
Definitionen III
Definition III.1 (Mittelpunkt einer Strecke)
Wenn ein Punkt  der Strecke
der Strecke  zu den Endpunkten
zu den Endpunkten  und
und  jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke
jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke  .
.
Definitionen IV
Definition IV.1 (offene Halbebene)
Es sei  eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen  und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
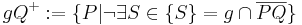 oder
oder 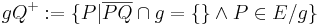
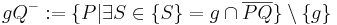 oder
oder 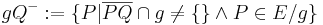 oder
oder 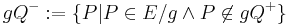
Definition IV.2 (Halbebene)
Es sei  eine Gerade der Ebene
eine Gerade der Ebene  .
.  und
und 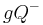 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
Definition IV.3: (konvexe Punktmenge)
Eine Menge  von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
Definitionen V
Definition V.1 (Winkel)
Unter einem Winkel 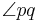 versteht man die Vereinigungsmenge zweier Strahlen p und q mit einem gemeinsamen Anfangspunkt S. Die beiden Strahlen sind die Schenkel des Winkels
versteht man die Vereinigungsmenge zweier Strahlen p und q mit einem gemeinsamen Anfangspunkt S. Die beiden Strahlen sind die Schenkel des Winkels 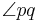 . Der gemeinsame Anfangspunkt der beiden Strahlen heißt Scheitelpunkt S
. Der gemeinsame Anfangspunkt der beiden Strahlen heißt Scheitelpunkt S
Definition V.2 (Inneres eines Winkels)
Unter dem Inneren eines Winkels  versteht man die Schnittmenge zweier Halbebenen ASB+ und BSA+.
versteht man die Schnittmenge zweier Halbebenen ASB+ und BSA+.
Definition V.3 (Scheitelwinkel)
(a) Zwei Winkel sind Scheitelwinkel, wenn deren Schenkel ein Paar sich schneidender Geraden bilden.
(b) Die Winkel 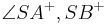 und
und 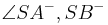 sind Scheitelwinkel.
sind Scheitelwinkel.
Definition V.4 (Nebenwinkel)
(a) Zwei Winkel sind Nebenwinkel, wenn sie einen Schenkel gemeinsam haben und die beiden anderen Schenkel eine Gerade bilden.
(b) Die Winkel 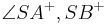 und
und 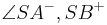 sind Nebenwinkel.
sind Nebenwinkel.
Definition V.5 (Größe eines Winkels)
Die Zahl 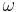 , die entsprechend des Winkelmaßaxioms einem jeden Winkel
, die entsprechend des Winkelmaßaxioms einem jeden Winkel  eindeutig zugeordnet werden kann, wird die Größe oder das Maß von
eindeutig zugeordnet werden kann, wird die Größe oder das Maß von  genannt.
genannt.
In Zeichen: 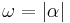 .
.
Definition V.6 : (Rechter Winkel)
Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition V.7 : (Supplementärwinkel)
Zwei Winkel heißen supplementär, wenn die Summe ihrer Größen 180 beträgt.
Definition V.8 : (Relation senkrecht auf der Menge der Geraden)
Es seien  und
und  zwei Geraden. Wenn sich
zwei Geraden. Wenn sich  und
und  schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden
schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden  und
und  senkrecht aufeinader.
senkrecht aufeinader.
In Zeichen: 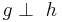
Definition V.9 (noch mehr Senkrecht)
1. Eine Gerade  und eine Strecke
und eine Strecke  stehen senkrecht aufeinander, wenn die
stehen senkrecht aufeinander, wenn die  und die Gerade
und die Gerade  senkrecht aufeinander stehen.
senkrecht aufeinander stehen.
2. Eine Strecke  und eine Strecke
und eine Strecke 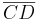 stehen senkrecht aufeinander, wenn die Gerade
stehen senkrecht aufeinander, wenn die Gerade  senkrecht auf der Geraden
senkrecht auf der Geraden 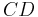 steht.
steht.
3. Eine Gerade  und eine Ebene
und eine Ebene  stehen senkrecht aufeinander, wenn es in
stehen senkrecht aufeinander, wenn es in  zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen--Engel82 12:50, 8. Dez. 2010 (UTC)
zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen--Engel82 12:50, 8. Dez. 2010 (UTC)
Defintionen VI
Definition VI.1 (Mittelsenkrechte)
Es sei  eine Gerade und
eine Gerade und  eine Strecke, die durch
eine Strecke, die durch  im Punkt
im Punkt  geschnitten wird.
geschnitten wird.  ist die Mittelsenkrechte von
ist die Mittelsenkrechte von  , wenn
, wenn
Definition VI.2 (Winkelhalbierende)
(a) Es sei ASB ein Winkel und SP+ ein Strahl, der vollständig im Inneren vom Winkel ASB liegt. Der Strahl SP+ heißt Winkelhalbierende des Winkels ASB, falls die Winkel ASP und PSB dieselbe Größe haben.
(b) Es seien  ,
,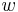 und
und 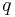 drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt
drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt  . Die Halbgerade
. Die Halbgerade 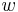 ist die Winkelhalbierende des Winkels
ist die Winkelhalbierende des Winkels 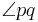 , wenn
, wenn 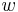 im Inneren von
im Inneren von 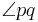 liegt und die beiden Winkel
liegt und die beiden Winkel 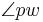 und
und 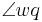 dieselbe Größe haben.
dieselbe Größe haben.
Definitionen VII
Definition VII.1 (Streckenkongruenz)
Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
In Zeichen 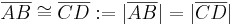
Definition VII.2 (Winkelkongruenz)
Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
In Zeichen: 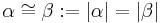
Definition VII.3 (Dreieckskongruenz)
Wenn für zwei Dreiecke  und
und  die folgenden 6 Kongruenzen
die folgenden 6 Kongruenzen
gelten,
dann sind die beiden Dreiecke  und
und  kongruent zueinander.
kongruent zueinander.
Definition VII.4 (gleichschenkliges Dreieck, Schenkel, Basis, Basiswinkel)
Ein gleichschenkliges Dreieck ist ein Dreieck bei dem zwei Seiten zueinander kongruent sind.
Ein Schenkel ist eine der kongruenten Seiten des gleichschenkligen Dreiecks.
Die dritte Seite nennt man Basis des gleichschenkligen Dreiecks.
Der Winkel, der die Basis als Teilmenge hat nennt man Basiswinkel des gleichschenkligen Dreiecks.
Definitionen VIII
Definition VIII.1 (Außenwinkel eines Dreiecks) =
Gegeben sei ein Dreieck  . Alle Nebenwinkel der Innenwinkel des Dreiecks
. Alle Nebenwinkel der Innenwinkel des Dreiecks  heißen Außenwinkel des Dreiecks
heißen Außenwinkel des Dreiecks  .
.
Definitionen IX
Definition IX.1 (Lot, Lotgerade, Lotfußpunkt)
Es sei  ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge.
gehören möge.
Eine Gerade  mit
mit 
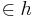 und
und 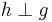 heißt Lot/Lotgerade vom Punkt
heißt Lot/Lotgerade vom Punkt  auf die Gerade
auf die Gerade  und der Punkt
und der Punkt  mit {
mit { } =
} = 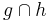 heißt Lotfußpunkt des Lotes von
heißt Lotfußpunkt des Lotes von  auf
auf  .
.
Definition IX.2 (Abstand eines Punktes zu einer Geraden)
Es sei  ein Punkt außerhalb von
ein Punkt außerhalb von  .
.
Der Abstand von  zu
zu  ist der Abstand der Punkte
ist der Abstand der Punkte  und
und  , wobei L der Lotfußpunkt des Lotes von
, wobei L der Lotfußpunkt des Lotes von  auf
auf  ist.
ist.