Lösung von Aufgabe 3.3 (SoSe11)
Aus Geometrie-Wiki
Version vom 19. April 2011, 13:24 Uhr von Schnirch (Diskussion | Beiträge)
Wir gehen von folgender Definition aus:
Eine Winkelhalbierende eines Winkels  ist ein Strahl l, der im Inneren des Winkels
ist ein Strahl l, der im Inneren des Winkels  liegt, den Scheitel des Winkels
liegt, den Scheitel des Winkels  als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel
als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel 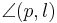 und
und 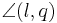 unterteilt.
unterteilt.
Außerdem sei folgende genetische Definition gegeben:
- Gegeben sei ein Winkel
 .
.
- Man konstruiere auf den beiden Schenkeln des Winkels
 zwei Punkte P und Q, die vom Scheitel S des Winkels
zwei Punkte P und Q, die vom Scheitel S des Winkels  gleich weit entfernt sind.
gleich weit entfernt sind.
- Man konstruiere die Strecke
 .
.
- Man konstruiere den Mittelpunkt M der Strecke
 .
.
- Man konstruiere den Strahl w mit dem Anfangspunkt S, der durch den Punkt M verläuft.
- Dieser Strahl w ist die Winkelhalbierende.
Beweisen Sie, dass durch diese Konstruktionsvorschrift tatsächlich die Winkelhalbierende entsprechend der angegebenen Definition entsteht.

