Lösung von Aufg. 9.1 (SoSe 11)
Aus Geometrie-Wiki
Version vom 7. Juni 2011, 16:36 Uhr von Bubble (Diskussion | Beiträge)
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Kann mir jemand helfen? Ich weiß nicht, was Voraussetzung und was Behauptung ist in diesem Beweis. Kann es sein, dass die Behauptung aus zwei Teilen besteht 1)  und 2)
und 2)  ?
?
Verwendet man hier das Abstandsaxiom und ist dabei der Abstand d = 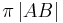 ?
?
Vielen Dank schonmal :) --Bubble 17:36, 7. Jun. 2011 (CEST)

