Lösung von Aufg. 11.6 (SoSe 11)

Definition V.9 : (noch mehr Senkrecht)

Eine Gerade $\ g$ und eine Strecke $\overline{AB}$ stehen senkrecht aufeinander, wenn die $\ g$ und die Gerade $\ AB$ senkrecht aufeinander stehen.

Ergänzen Sie:

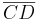Eine Strecke $\ \overline{AB}$ und eine Strecke $\ \overline{CD}$ stehen senkrecht aufeinander, wenn ... .

Eine Gerade $\ g$ und eine Ebene $\epsilon$ stehen senkrecht aueinander, wenn es in $\epsilon$ ... .

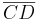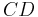Eine Strecke $\ \overline{AB}$ und eine Strecke $\ \overline{CD}$ stehen senkrecht aufeinander, wenn die Gerade $\ AB$ und die Gerade $\ CD$ senkrecht aufeinander stehen (auch wenn die Strecken keinen gemeinsamen Punkt haben).

Eine Gerade $\ g$ und eine Ebene $\epsilon$ stehen senkrecht aueinander, wenn es in $\epsilon$ mindestens zwei verschiedene Geraden gibt, die senkrecht auf g stehen. --WikiNutzer 14:40, 7. Jul. 2011 (CEST)