Lösung von Aufgabe 6.6 (SoSe 11)

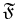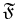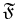Es sei $\ \mathfrak{F}$ die Menge der Figuren der Ebene. Auf $\ \mathfrak{F}$ sei eine Äquivalenzrelation $\ \Theta$ definiert. $\ \Theta$ möge $\ \mathfrak{F}$ derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
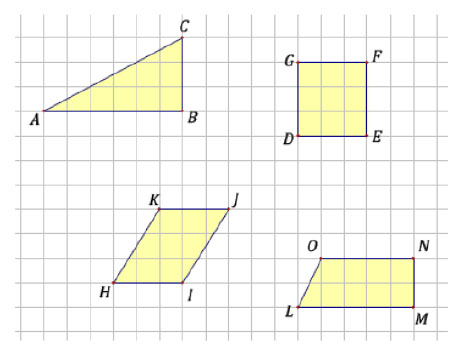
Geben Sie mögliche Interpretationen der Relation $\ \Theta$ an.

- sind konvex
- liegen in der gleichen Ebene wie

- haben den gleichen Flächeninhalt --Madita 15:24, 19. Mai 2011 (CEST)

Die Antwort: "haben den gleichen Flächeninhalt" ist korrekt, die Antwort: "sind konvex" ist problematisch. Erkennen Sie den prinzipiellen
 Unterschied zwischen den beiden Antworten?--Schnirch 14:27, 9. Jun. 2011 (CEST)

konvex wäre doch dann möglich, wenn das Dreieck nicht dabei wäre? Dreicke sind doch immer konvex, dann würde die Def. von Madita alle Dreiecke mit einschließen...--mm_l 11:51, 14. Jul. 2011 (CEST)
Dreiecke sind immer konvex, das ist richtig. Deshalb tritt hier kein Problem auf, dies liegt wo anders.

Überlegt euch nochmal den Unterschied der Begriffe Relation und Klasse.
Ein Beispiel:
Eine Menge an Wäscheklammern lässt sich in Klassen einteilen. Z.B. die Klasse der roten, grünen, blauen... Wäscheklammern. Sind zwei Wäscheklammern in einer Klasse, so stehen sie in Relation. Diese kann man dann "hat gleiche Farbe wie" nennen.'

Was ist bei "sind konvex" problematisch und wie könnte man es dann sagen?
--Tutorin Anne 22:01, 14. Jul. 2011 (CEST)
Eine Figur ist entweder konvex oder konkav. Somit gibt es die Klasse der konvexen und der konkaven Figuren. Aber es wird dabei keine Relation zueinander angegeben wie z.B. "ist konvex wie".--Katrin 09:37, 15. Jul. 2011 (CEST)