Der Inkreis und die Winkelhalbierenden eines Dreiecks (SoSe 11)

Winkelhalbierenden eines Dreiecks

Definition XV.1 : (Winkelhalbierenden eines Dreiecks)

Unter den Winkelhalbierenden eines Dreiecks versteht man die Winkelhalbierenden der Innenwinkel des Dreiecks.

Satz XV.1a : (Abstand eines Punktes einer Winkelhalbierenden zu den Schenkeln des Winkels)

Jeder Punkt der Winkelhalbierenden eines Winkels hat zu den Schenkeln des Winkels jeweils ein und denselben Abstand.

Satz XV.1b : (Umkehrung von Satz XV.1a)

(das können Sie selbst:)

Jeder Punkt im Inneren eines Winkels, der zu den Schenkeln jeweils denselben Abstand hat, ist die Winkelhalbierende des Winkels. --Teufelchen 15:53, 12. Jul. 2011 (CEST)

schreiben Sie besser: ...gehört zur Winkelhalbierenden des
 Winkels. Nach Ihrer Formulierung könnte sonst eine Winkelhalbierende aus einem einzigen Punkt
 bestehen.--Schnirch 14:27, 17. Jul. 2011 (CEST)

Winkelhalbierendenkriterium

(auch das sollten Sie jetzt selbst hinbekommen:)

Der Strahl 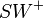$\ SW^{+}$ ist genau dann Winkelhalbierende des Winkels $\angle ASB$ , wenn jeder Punkt der Winkelhalbierenden zu den Schenkeln ein und denselben Abstand hat. --Teufelchen 23:24, 11. Jul. 2011 (CEST)

schreiben Sie besser: ...wenn jeder Punkt des Strahls zu den
 Schenkeln..., denn Sie wollen ja die Bedingung beschreiben, die für den Strahl gelten muss, damit er
 Winkelhalbierende ist--Schnirch 14:36, 17. Jul. 2011 (CEST)

oder
Genau dann, wenn jeder Punkt der zu den Schenkeln eines Winkels ein und denselben Abstand hat, dann liebt die Winkelhalbierenden im Inneren des Winkels. --Teufelchen 16:02, 12. Jul. 2011 (CEST)

Versuchen Sie doch mal die folgende Formulierung zu vervollständigen:--Schnirch 14:41, 17. Jul. 2011 (CEST)
Es sei P ein Punkt aus dem Inneren des Winkels $\alpha$. P ist genau dann ein Punkt der...

Es sei P ein Punkt aus dem Inneren des Winkels $\alpha$. P ist genau dann ein Punkt der Winkelhalbierenden, wenn er zu den beiden Schenkeln des Winkels $\alpha$ ein und denselben Abstand hat.--Bushido

Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks)

Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.

Beweis von Satz XV.2 mit Hilfe des Winkelhalbierendenkriteriums: Versuchen Sie es selbst:

Inkreis eines Dreiecks

Definition XV.2 : (Tangente an einen Kreis)

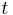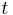Eine Gerade $\ t$ berührt einen Kreis $\ k$, wenn sie mit dem Kreis $\ k$ genau einen Punkt $\ P$ gemeinsam hat. Die Gerade $\ t$ heißt Tangente im Punkt $\ P$.
es musst noch ergänzt werden, dass der Punkt P Berührpunkt heißt. Mathegott 16:53, 19. Jul. 2011 (CEST)

Definition XV.3 : (Strecke berührt Kreis)

Eine Strecke $\overline{AB}$ berührt einen Kreis $\ k$, wenn sie... (ergänzen Sie!)

Teilmenge der Tangente AB des Kreises ist. --Teufelchen 16:22, 13. Jul. 2011 (CEST)

Das kann stimmen, gilt aber nicht allgemein.--Tutorin Anne 19:46, 18. Jul. 2011 (CEST)

Eine Strecke AB berührt einen Kreis k, wenn sie Teilmenge der Tangente AB des Kreises k ist und der Berührpunkt zu der Strecke AB gehört.Mathegott 16:53, 19. Jul. 2011 (CEST)

Definition XV.4 : (Inkreis eines Dreiecks)

Ein Kreis, der alle drei Seiten eines Dreiecks in jeweils genau einem Punkt berührt, heißt Inkreis des Dreiecks.

Satz XV.3 : (Existenz und Eindeutigkeit des Inkreises)

...ergänzen Sie!

Jedes Dreieck hat genau einen Inkreis.--Teufelchen 23:26, 11. Jul. 2011 (CEST)