Definition der Woche 10 (SoSe 11)

Die folgende Abbildung zeigt den schematischen Aufbau eines Wankelmotors. Der sich drehende "Kolben" hat dabei die Form eines sogenannten Reuleauxdreiecks.

Definieren Sie den Begriff Reuleauxdreieck.

Zunächst sei angemerkt, dass das Ding hier sau schwer ist (im ernst, so ein Wankelmotorblock wiegt schon so seine Kilos :-) ).
Da wir es hier mit einem kleinen Zahnrad zu tun haben, über das ein größeres läuft, können wir hier evtl. mit den Hypozykloiden definieren.
Definition Motorblock (auch wenn das hier nicht gefragt ist):

Sei A ein Zahnrad und B ein Zahnrad, für das gilt, dass die Anzahl der Zähne in A genau 2/3 der Anzahl von B entsprechen. Ferner sei N ein beliebiger Punkt im inneren von A mit N $\neq$ Mittelpunkt von A.

Das Hypozykloid, welches die Form eines Wankelmotorblocks hat, ist die Menge aller Punkte P, für die gilt, dass |NP| = |RadiusA| + |RadiusB| + x, wobei x = fab.

Hier der "Beweis" (auch wenn man Definitionen nicht beweisen kann, deshalb in ""):

Datei:Hypozykloid.JPG
Jetzt das Dreick:

Intuitiv: Ein Reuleauxdreieck ist ein Dreieck, das so aussieht wie ein Querschnitt von Stabilo Trio Scribble Stiften.

Ein bischen informeller: Ein Reuleaudreieck ist die Schnittmenge einer Ebene E mit einem Stabilo Trio Scribble Stift. Die Ebene schneidet den Stift parallel zur Grundfläche von Stabilo Trio Scribble.

Ein bischen formaler: Ein Reuleaudreieck ist ein konvexes Dreieck dessen drei Seiten je ein und die selbe Krümmung haben.

Mathematisch, formal korrekt: Sei \overline{ABC} ein konvexes Dreieck, dessen Seiten kongruent zueinander sind. Wenn die Seiten von \overline{ABC} derart gekrümmt sind, dass sie keine Strecke zwischen ihren Endpunkten bilden, dann ist das Dreieck ein Reuleaudreieck.

Naja ob das jetzt so formal korrekt ist sei dahingestellt. --Flo60 11:46, 25. Jun. 2011 (CEST) Ich werd mir auf alle Fälle keinen Mazda kaufen - da sind die Dinger nämlich drin und jetzt ist mir die Freude am Wankelmotor (der Erfinder ist übrigens auf dem Bergfriedhof in HD beerdigt worden) vergangen. :-)

ein wenig Hilfe

--*m.g.* 16:15, 26. Jun. 2011 (CEST)

Krümmung

Die Idee mit der Krümmung ist gut. Klar, wir haben ein Dreieck dessen Seiten keine Strecken sind. Wären es Strecken, dann hätte jeder Punkt dieser Strecke die Krümmung 0. Jeder Punkt einer ebenen Kurve hat eine ihm zugeordnete Krümmung. In der Regel haben zwei verschiedene Punkte einer Kurve auch zwei verschiedene Werte, die ihnen als Krümmung zuzuordnen sind: Krümmung. Es gibt jedoch auch Kurven, bei denen mehrere Punkte ein und dieselbe Krümmung haben. So haben etwa alle Punkte ein und desselben Kreises dieselbe Krümmung. Hätten wir Krümmung sauber definiert, könnten wir den begriff Kreis wie folgt definieren: Ein Kreis ist eine ebene Kurve mit konstanter Krümmung. Die Punkte eines größeren Kreises haben eine geringere Krümmung als die Punkte eines kleineren Kreises. Die Krümmung eines Kreises lässt sich dementsprechend wie folgt definieren: Es sei 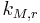$k_{M,r}$ ein Kreis. Die Krümmung von 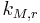$k_{M,r}$ ist die Zahl $\frac{1}{r}$.

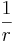Sie haben richtig erkannt, dass jeder Punkt der Seiten unseres Reuleauxdreiecks dieselbe Krümmung hat. Sie sind also Teile eines Kreises. Anders ausgedrückt: Die "Seiten" eines Reuleauxdreiecks sind Teile von Kreisen.

Mazda

Nur im Mazda RX8 (und seinen Vorgängern) werkelt ein Wankelmotor. Legendär war der NSU RO 80: NSU_Ro_80.

Damals hatte sogar versucht in den Trabbi einen Wankelmotor einzubauen.

Felix Wankel

Felix_Wankel

Motorform als Hypo- bzw. Epizykloide

Rollkurven#Wankelmotor

Es sei ABC ein gleichseitiges Dreieck, x sei die Seitenlänge des Dreiecks. Unter einem Reuleauxdreieck versteht man die Kreisbögen durch je zwei Eckpunkte des Dreiecks ABC mit dem dritten Punkt als Mittelpunkt und dem Radius x.--Verteidigungswolf 13:44, 23. Jul. 2011 (CEST)