12)
Aus Geometrie-Wiki
Version vom 28. November 2011, 14:16 Uhr von Wookie (Diskussion | Beiträge)
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Voraussetzung: Gerade g, Punkt P: P 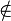 g
g
Behauptung: 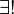 Ebene E: g
Ebene E: g  E
E  P
P  E
E
Beweis:
1) P 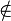 g g |
Vor. |
2)  R, Q R, Q  g, R g, R Q Q |
Axiom I/2 |
| 3) nkoll(P, Q, R) | Axiom I/3, 1), 2) |
4) 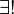 E: (P, Q, R) E: (P, Q, R) E E |
Axiom I/4, 3) |
5) P  E E  g g 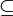 E E |
4) |

