Aufgabe 4.1
Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler.
(a) Eine dieser Relationen ist keine Äquivalenzrelationen. Welche? Beweisen Sie Ihre Aussage.
(b) Beweisen Sie für die andere Relation, dass sie eine Äquivalanzrelation ist.
Aufgabe 4.2
Die Gleichung 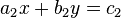 ist eine Linearkombination der Gleichung ist eine Linearkombination der Gleichung 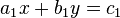 , wenn eine Zahl , wenn eine Zahl 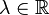 derart existiert,
dass derart existiert,
dass
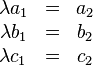
gilt.
(a) Beweisen Sie: Die Relation Gleichung b ist Linearkombination von Gleichung a ist eine Äquivalenzrelation auf der Menge der Gleichungen vom Typ  . .
(b) Interpretieren Sie die Relation geometrisch.
Aufgabe 4.3
Es sei 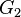 die Menge aller Gleichungen vom Typ die Menge aller Gleichungen vom Typ  . . 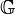 sei die Menge aller Äquivalenzklassen sei die Menge aller Äquivalenzklassen 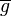 , in die , in die  durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf 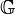 die folgende Operation die folgende Operation  : : 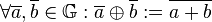 . Beweisen Sie: . Beweisen Sie: ![[\mathbb{G}, \oplus]](/images/math/f/9/7/f973823fb9e00ff432d68505910909a8.png) ist Gruppe. ist Gruppe.
Aufgabe 4.4
Es sei  die Menge der natürlichen Zahlen ohne die Zahl die Menge der natürlichen Zahlen ohne die Zahl 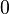 . Wir definieren . Wir definieren 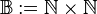 . Auf . Auf 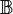 definieren wir die folgende Relation quotientengleich definieren wir die folgende Relation quotientengleich 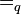 : : 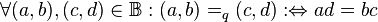 . Beweisen Sie . Beweisen Sie 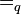 ist eine Äquivalenzrelation. ist eine Äquivalenzrelation.
Aufgabe 4.5
Es sei 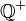 die Menge aller Äquivalenzklassen die Menge aller Äquivalenzklassen 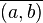 in die in die 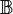 durch durch 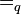 eingeteilt wird. Wir definieren eingeteilt wird. Wir definieren 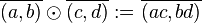 . Beweisen Sie: . Beweisen Sie: ![[\mathbb{Q}^+, \odot]](/images/math/b/d/8/bd820b10ad4122ad5c5c8b8d1600aff7.png) ist abelsche Gruppe. ist abelsche Gruppe.
Aufgabe 4.6
Beweisen Sie: Die multiplikative Restklassengruppe modulo 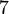 ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe. ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.
Aufgabe 4.7
Nennen Sie eine multiplikative zyklische Gruppe, die genau vier erzeugende Elemente hat.
Aufgabe 4.8
Wir betrachten ![[\mathbb{R}, +]](/images/math/b/c/d/bcda2db217cbfafb8f4e992cc54382c2.png) , die additive Gruppe der reellen Zahlen. Unter , die additive Gruppe der reellen Zahlen. Unter 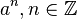 verstehen wir somit das verstehen wir somit das 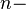 malige Aufaddieren von malige Aufaddieren von 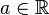 . . 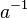 ist damit das inverse Element von ist damit das inverse Element von  bzgl. der Addition reeller Zahlen. bzgl. der Addition reeller Zahlen.
Mittels dieser Potenzierung definieren wir für den 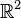 : : 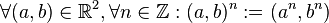 . .
Es sei 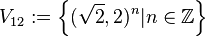 . Beweisen Sie, dass . Beweisen Sie, dass ![\left [V_{12},\oplus \right ]](/images/math/8/4/5/845dd551d7abca7d64d41825e0a0de03.png) eine abelsche Gruppe ist. Unter eine abelsche Gruppe ist. Unter  verstehen wir dabei die übliche additive Verknüpfung von Elementen des verstehen wir dabei die übliche additive Verknüpfung von Elementen des 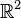 . .
Aufgabe 4.9
Beweisen Sie: Jede zyklische Gruppe ist abelsch.
Aufgabe 4.10
Es sei ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png) die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf 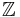 . . ![[2\mathbb{Z}, +]](/images/math/2/e/e/2ee302fb5c070ca301bdf2fd7583d492.png) sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf 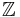 . Wir definieren eine Abbildung . Wir definieren eine Abbildung  von von 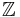 auf auf 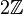 : : 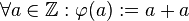 . .
(a) Beweisen Sie:  ist eine Bijektion ist eine Bijektion
(b) 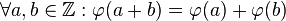 . .
| 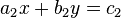 ist eine Linearkombination der Gleichung
ist eine Linearkombination der Gleichung 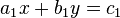 , wenn eine Zahl
, wenn eine Zahl 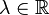 derart existiert,
dass
derart existiert,
dass 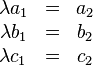
 .
.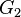 die Menge aller Gleichungen vom Typ
die Menge aller Gleichungen vom Typ 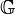 sei die Menge aller Äquivalenzklassen
sei die Menge aller Äquivalenzklassen 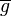 , in die
, in die  durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf
durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf  :
: 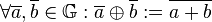 . Beweisen Sie:
. Beweisen Sie: ![[\mathbb{G}, \oplus]](/images/math/f/9/7/f973823fb9e00ff432d68505910909a8.png) ist Gruppe.
ist Gruppe.
 die Menge der natürlichen Zahlen ohne die Zahl
die Menge der natürlichen Zahlen ohne die Zahl 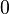 . Wir definieren
. Wir definieren 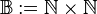 . Auf
. Auf 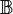 definieren wir die folgende Relation quotientengleich
definieren wir die folgende Relation quotientengleich 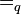 :
: 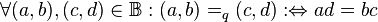 . Beweisen Sie
. Beweisen Sie 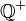 die Menge aller Äquivalenzklassen
die Menge aller Äquivalenzklassen 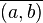 in die
in die 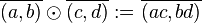 . Beweisen Sie:
. Beweisen Sie: ![[\mathbb{Q}^+, \odot]](/images/math/b/d/8/bd820b10ad4122ad5c5c8b8d1600aff7.png) ist abelsche Gruppe.
ist abelsche Gruppe.
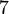 ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.
ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.
![[\mathbb{R}, +]](/images/math/b/c/d/bcda2db217cbfafb8f4e992cc54382c2.png) , die additive Gruppe der reellen Zahlen. Unter
, die additive Gruppe der reellen Zahlen. Unter 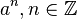 verstehen wir somit das
verstehen wir somit das 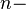 malige Aufaddieren von
malige Aufaddieren von 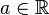 .
. 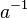 ist damit das inverse Element von
ist damit das inverse Element von  bzgl. der Addition reeller Zahlen.
bzgl. der Addition reeller Zahlen.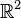 :
: 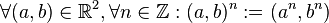 .
.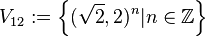 . Beweisen Sie, dass
. Beweisen Sie, dass ![\left [V_{12},\oplus \right ]](/images/math/8/4/5/845dd551d7abca7d64d41825e0a0de03.png) eine abelsche Gruppe ist. Unter
eine abelsche Gruppe ist. Unter ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png) die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf
die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf 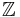 .
. ![[2\mathbb{Z}, +]](/images/math/2/e/e/2ee302fb5c070ca301bdf2fd7583d492.png) sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf
sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf  von
von 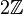 :
: 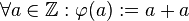 .
. 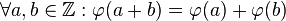 .
.

