Ausgefüllte Übungsklausuren bzw. Lösungen Serie 9 SoSe 2020
Laden Sie hier oder auf StudIP Ihre bearbeiteten Übungsklausuren hoch.
Inhaltsverzeichnis |
Bemerkungen zu eingereichten Lösungen
Definitionen
Aufgabe 9.1 a)
Definieren Sie den Begriff Viereck. (n-Eck sei noch nicht definiert.)
Definition 1
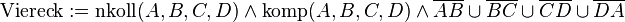
oder
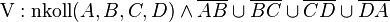
Bemerkungen zu Definition 1
sprachliche Formulierung
Beide Definitionen entsprechen nicht dem Niveau, das zu veranschlagen wäre. Sie müssen eine vollständige formal korrekte Definition abliefern. Die Variante Begriffsbezeichnung:=Aufzählung von Eigenschaften ist keine vollständige Definition. Sie dürfen mathematisch formal mittels mathematischer Symbole formulieren. Das müssen Sie dann aber auch korrekt beherrschen.
Definition: (Viereck)
- Ein Viereck V ist die folgende Punktmenge
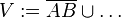
- Ein Viereck V ist die folgende Punktmenge
Sie können nicht einfach irgendein ungeklärtes Zeichen nehmen und nach einem Doppelpunkt Dinge aufzählen, die mit dem Begriff zu tun haben.
Zum Vergleich: Im Kontext juristischer Gesetze wird festgelegt was Raub ist.
Raub
- R: gehört dir nicht
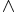 nimmste trotzdem
nimmste trotzdem
sprachliche Formulierung aus der Sicht mathematischer Logik
Das Zeichen 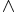 steht für das mathematische UND. Das mathematische UND ist eine Verknüpfung zweier Aussagen und ist nicht mit dem aufzählenden und der deutschen Sprache zu verwechseln.
steht für das mathematische UND. Das mathematische UND ist eine Verknüpfung zweier Aussagen und ist nicht mit dem aufzählenden und der deutschen Sprache zu verwechseln.
- aufzählendes und der deutschen Sprache:
- Wir kaufen einen Kasten Hefeweizen und einen Kasten Pils
- Das Auto hat einen Bremsassistenten und Halogenscheinwerfer
- mathematisches UND: Verknüpfung zweier Aussagen
- 6 ist durch 2 teilbar UND 6 ist durch 3 teilbar
- Aussage 1: 6 ist durch 2 teilbar
- Aussage 2: 6 ist durch 3 teilbar
- Verknüpfung: Aussage 1 und Aussage 2
Merke: Durch UND 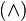 können nur mathematische Aussagen verknüpft werden. Die Mathematiker sind schlichten Gemüts und haben fest gelegt, dass es für mathematische Aussagen nur die Wahrheitwerte Wahr oder Falsch geben kann. Sie erkennen, ob eine mathematische Formulierung eine Aussage ist daran, dass der Formulierung eindeutig ein Wahrheitswert zugewiesen werden kann:
können nur mathematische Aussagen verknüpft werden. Die Mathematiker sind schlichten Gemüts und haben fest gelegt, dass es für mathematische Aussagen nur die Wahrheitwerte Wahr oder Falsch geben kann. Sie erkennen, ob eine mathematische Formulierung eine Aussage ist daran, dass der Formulierung eindeutig ein Wahrheitswert zugewiesen werden kann:
| Formulierung | Wahrheitswert | Aussage? |
|---|---|---|
| ein Sack Kartoffeln | nicht bestimmbar | nein |
| ein Sack neuer Kartoffeln | nicht bestimmbar | nein |
| Im Keller steht ein Sack neuer Kartoffeln. | ist entweder wahr oder falsch, müssen wir im Keller überprüfen | ja |
| die Schnittmenge einer Ebene mit einem unendlich hohen Zylinder | kein Wahrheitswert | nein |
| Die Schnittmenge einer Ebene mit einem unendlich hohen Zylinder ist ein Kegelschnitt oder die leere Menge. | wahr | ja |
Verknüpfungen:
-
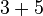 geht in Ordnung, zwei Zahlen werden mittels Plus miteinander verknüpft
geht in Ordnung, zwei Zahlen werden mittels Plus miteinander verknüpft
-
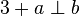 Das ist völlig sinnlos. Man kann nicht sinnvoll die Aussage a steht senkrecht auf b zur Zahl 3 addieren
Das ist völlig sinnlos. Man kann nicht sinnvoll die Aussage a steht senkrecht auf b zur Zahl 3 addieren
- Ein Sack Kartoffeln UND soziale Unruhen in den USA Diese Verknüpfung durch das mathematische UND ist völlig sinnlos. Es können nur Aussagen verknüpft werden. weder ein Sack Kartoffeln noch soziale Unruhen in den USA sind Aussagen
- Im Keller von Familie Maier steht ein Sack Kartoffeln. UND Es gibt derzeit soziale Unruhen in den USA. Beide Teilaussagen sind wahr, Die Gesamtaussage damit auch.
- Die Punkte A, B, C und D sind nicht kollinear. UND Die Vereinigungsmenge der vier Strecken
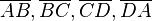 . Diese Verknüpfung durch das mathematische UND ist genauso sinnlos wie
. Diese Verknüpfung durch das mathematische UND ist genauso sinnlos wie
- Der Tisch ist grün. UND ein Sack Kartoffeln.
Quintessenz: Man darf Aussagen nicht mit Punktmengen durch UND verknüpfen.
Wie geht es dann?
Formulieren Sie eine "Opernführerdefinition" :
- Es seien
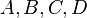 vier Punkte, die komplanar und von denen je drei immer nicht kollinear sind. Die Vereinigungsmenge aus den Strecken
vier Punkte, die komplanar und von denen je drei immer nicht kollinear sind. Die Vereinigungsmenge aus den Strecken 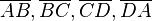 heißt Viereck
heißt Viereck  .
.
- Es seien

