Lösung von Aufg. 7.3P (SoSe 22)

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

$\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace\Rightarrow \overline{AC}\cap g=\lbrace \rbrace$

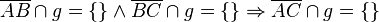
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 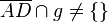$\overline{AD}\cap g\not=\lbrace \rbrace$ und nutzen Sie den Satz von Pasch)
Voraussetzung :drei paarweise verschiedene und kolineare Punkte A,B und C in einer Ebene E. Strecke AB geschnitten g und Strecke BC geschnitten g ergibt leere Menge, Gerade g teilt die Ebene E in zwei Halbebenen Behauptung: Stecke AC geschnitten g ergibt leere Menge

ich brauche hier einen Punkt D, der auf der anderen Halbebene liegt, in dem nicht die Punkte A,B, C liegen und verbinde dann die Punkte ABD, BCD und ACD zu jeweils einem Dreieck, welche alle die Gerade g schneiden und somit die Strecke AD, BD und CD geschnitten g keine leere Menge ergeben.

Beweisschritt : 1. Strecke AB geschnitten g ergibt leere Menge, Begründung: Voraussetzung
                2. Strecke BC geschnitten g ergibt leere Menge, Begründung: Voraussetzung
                3. g teilt die Ebene in zwei Halbebenen  ; Begründung : Vorausseztung
                4. Punkt D liegt auf der anderen Halbebene und ist nicht kolinear zu A,B,C, Begründung: wegen 3.,  Definition Ebene, 
                5. Strecke AD geschnitten g ergibt keine leere Menge, Begründung : wegen 3.,4. und Satz von Pasch, Def. Halbenene
                6. Strecke BD geschnitten g ergibt keine leere Menge, Begründung : wegen 3., 4. und Satz von Pasch, Def Halbebene
                7. Strecke CD geschnitten g ergibt keine leere Menge, Begründung: wegen 3., 4. und Satz von Pasch, Def Halbebene
                8. Strecke AC geschnitten g ergibt leere Menge, Begründung: wegen Voraussetzung, 3., 4. , 5., 6. 7.--Kwd077 (Diskussion) 11:35, 2. Jun. 2022 (CEST)

Der Beweis ist sehr gut. Die Begründung für Punkt 4 ergibt sich mir noch nicht ganz.--Matze2000 (Diskussion) 15:24, 12. Jun. 2022 (CEST)