Lösung von Aufgabe 1.3 (SoSe 20)

Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.

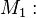$M_1:$ Menge aller gleichschenkligen Dreiecke

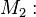$M_2:$ Menge aller gleichseitigen Dreiecke

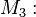$M_3:$ Menge aller gleichwinkligen Dreiecke

- Die Menge 2 und die Menge 3 sind identisch. - Die Menge 2 und die Menge 3 sind echte Teilmenge von Menge 1.--Elisa R. (Diskussion) 18:52, 18. Apr. 2020 (CEST)

- Die Mengen M_2 und M_3 sind identisch und M_1 ist eine echte Teilmenge von M_2 und M_3. --Kohfahlm (Diskussion) 17:26, 22. Apr. 2020 (CEST)

- m2=m3 / m1 teilmenge von m2 und m3--Durutti (Diskussion) 15:48, 23. Apr. 2020 (CEST)

Elisa R. hat die Teilmengenbeziehung richtig formuliert. $M_2$ = $M_3$ ⊂ $M_1$ 
Um dies zu verdeutlichen, kann man auch ein Venn-Diagramm dazu anfertigen. Wer möchte kann es gerne hochladen. --Tutorin Laura (Diskussion) 16:10, 23. Apr. 2020 (CEST)

- achja natürlich! dreiecke höherer ordnung (mit mehr symetrieeigenschaften) quasi immer teilmenge von dreicken nierigerer ordnung? wie beim haus der vierecke. also für dreiecke: 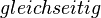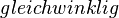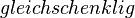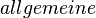$gleichseitig$ = $gleichwinklig$ ⊂ $gleichschenklig$ ⊂ $allgemeine$?--Durutti (Diskussion) 14:04, 24. Apr. 2020 (CEST)