Lösung von Aufgabe 1.4 (SoSe 17)

Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen.

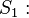$S_1:$ Menge aller Vierecke mit vier kongruenten Winkeln

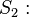$S_2:$ Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen

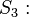$S_3:$ Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel

Ich würde sagen: S1= S2 und S1 c S 3 und S 2 c S 3

--Kissa052 (Diskussion) 12:18, 31. Mai 2017 (CEST)

→ → →

Ich glaube, dass 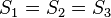$S_1 = S_2 = S_3$ gilt. Alles sind Definitionen für Rechtecke.

Bei 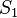$S_1$ ergibt sich das ziemlich direkt, denn nach dem Innenwinkelsatz können vier kongruente Winkel in einem Viereck nur 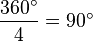$\frac{360^\circ}{4} = 90^\circ$ haben.

Bei $S_2$ bilden die Diagonalen mit den Seiten des Vierecks vier gleichschenklige Dreiecke, wobei jeweils zwei gegenüberliegende Dreiecke kongruent und somit alle Basiswinkel von je zwei gegenüberliegenden Dreiecken identisch sind. 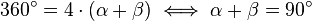Nennen wir die Basiswinkel des einen gegenüberliegenden Dreieckspaars $\alpha$, die des anderen Paars $\beta$, so ergibt sich die Innenwinkelsumme $360^\circ=4\cdot(\alpha + \beta) \iff \alpha + \beta = 90^\circ$, somit sind alle Innenwikel rechtwinklig.

Bei 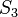$S_3$ kann man über Stufen- und Wechselwinkelsatz zeigen, dass bei einem Viereck mit zwei Paaren paralleler Gegenseiten jeweils gegenüberliegende Innenwinkel kongruent sind. Somit muss in solch einem Viereck gegenüber des gegebenen rechten Winkels noch ein rechter Winkel liegen. Da die beiden übrigen Winkel aber auch gegenüberliegend und somit gleich groß sind, teilen sich die beiden die restlichen 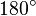$180^\circ$ bis zur Innenwinkelsumme vo 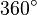$360^\circ$ auf, die die beiden rechten Winkel noch „übrig lassen“. Somit sind alle Winkel in diesem Viereck rechtwinklig. --AlanTu (Diskussion) 17:37, 31. Mai 2017 (CEST)

Hallo, 

oh, da war jemand schneller als ich^^ find ich gut, dass sich auch Studenten untereinander helfen ;) 
Zu AlanTu's Anmerkung habe ich nichts mehr hinzuzufügen, perfekt! 


--Tutor: Alex (Diskussion) 17:50, 31. Mai 2017 (CEST)