Lösung von Aufgabe 3.2 P (SoSe 12)

a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.
nahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?

_________________________
a)
Ein Dreieck, bei dem drei Seiten kongruent sind, heißt gleichseitiges Dreieck.
Ein Dreieck, bei dem zwei Seiten kongruent sind, heißt gleichschenkliges Dreieck.

b)
Information: Ich habe mich versucht an dem Beispiel in Übung 2 zu orientieren, weis aber nicht ob das so korrekt ist, weil ich einen Beweis durch Kontraposition noch nie zuvor gemacht habe!
(Ich hoffe, wir besprechen das Vorgehen bei einem Beweis durch Kontraposition in der Übung.)

Sei $\overline{ABC}$ ein Dreieck.
Vor: Gleichseitiges Dreieck (mit drei kongruenten Seiten)
Beh: Gleichschenkliges Dreieck (mit zwei kongruenten Seiten)
Bew:
Satz: gleichseitiges Dreieck $\Rightarrow$ gleichschenkliges Dreieck
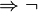Kontraposition: $\neg$ gleichschenkliges Dreieck $\Rightarrow \neg$ gleichseitiges Dreieck
Bei einem nicht gleichschenkligen Dreieck, müssen alle drei Seiten unterschiedlich lang sein bzw. keine der Seiten darf so lang sein, wie eine der anderen Seiten: 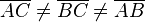$\overline{AC} \neq \overline{BC} \neq \overline{AB}$ . Keine der Seiten ist zu einer anderen Seite kongruent, also sind auch keine drei Seiten kongruent zueinander ($\neg$ gleichseitiges Dreieck).

von --Honeydukes 20:48, 4. Mai 2012 (CEST)

_________________________