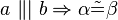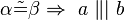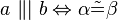Lösung von Aufgabe 3.3 (SoSe 13 P)

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel $\alpha$ und $\beta$. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

1. $\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta$

• Es fehlt der Bezug zur Gerade c.--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Diese Aussage repräsentiert den Stufenwinkelsatz.--Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
    • So ist es.--Tutorin Anne 21:42, 11. Mai 2013 (CEST)

1. $\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b$

• Umkehrung von (1). Gleiche Problematik wie in (1).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Hierbei handelt es sich um die Umkehrung der oberen Implikation. Eine Umkehrung des Stufenwinkelsatzes ist jedoch nicht möglich, daher ist diese Implikation weder repräsentativ noch äquivalent zum Stufenwinkelsatz.--Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
    • Gut begründet und nur noch ein Fehler.--Tutorin Anne 21:42, 11. Mai 2013 (CEST)
      • Komme nicht drauf.--Nolessonlearned 16:24, 12. Mai 2013 (CEST)
        
        • Die Aussage ist sehr wohl wahr. Sie muss aber extra bewiesen werden, da sie eben nicht äquivalent zum Stufenwinkelsatz ist.--Tutorin Anne 10:28, 23. Mai 2013 (CEST)

1. $\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b$

• Äquivalente Aussage zum Stufenwinkelsatz. Logischer Zusammenhang.--Nolessonlearned 16:59, 7. Mai 2013 (CEST)
  
  • Hierbei handelt es sich um eine Kontraposition zu dem Stufenwinkelsatz. --Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
  • Äquivalente Aussage zum Stufenwinkelsatz.--Nolessonlearned 18:18, 10. Mai 2013 (CEST)
    

 ** könnte jemand dies mal ohne Formelzeichen in einen Satz schreiben, ich versteh die ganzen Zeichen gar nicht und deswegen auch nicht die Aussage --Grashalm 11:36, 12. Jun. 2013 (CEST)

Hallo Grashalm, hier einmal in Worten:

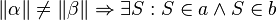1. $\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b$ bedeutet: Wenn das Maß des Winkels alpha ungleich dem Maß des Winkels beta, dann existiert ein Punkt S für den gilt: S ist element von a und S ist element von b.
   

Hilft dir das weiter?
--TobiWan 16:22, 12. Jun. 2013 (CEST)

ja vielen dank, nun kann ich es nachvollziehen :) --Grashalm 18:25, 12. Jun. 2013 (CEST)

1. $\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta$

• Selbe Problematik wie in (1) und (2).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Da eine Umkehrung des Stufenwinkelsatzes nicht möglich ist (siehe 2. Implikation), ist eine Äquivalenzrelation der beiden Aussagen ebenfalls ausgeschlossen.--Nolessonlearned 18:18, 10. Mai 2013 (CEST)
    
    • Mh, stimmt nicht ganz.--Tutorin Anne 21:42, 11. Mai 2013 (CEST
      )
      • Bräuchte etwas Hilfe. Komme nicht drauf. --Nolessonlearned 16:24, 12. Mai 2013 (CEST)
        
        • Siehe 2)--Tutorin Anne 10:28, 23. Mai 2013 (CEST)
          • Wenn man also die 2.Implikation beweist, dann gilt auch diese Äquivalenzrelation oder? --Zweieck 14:03, 30. Mai 2013 (CEST)
            • So ist es.--Tutorin Anne 18:24, 2. Jun. 2013 (CEST)

Also zusammenfassend habe ich das jetzt so verstanden|:

1.) Stufenwinkelsatz
2.) Umkehrung des Stufenwinkelsatzes; aber nicht gültig, da noch nicht bewiesen
3.) Kontraposition des Stufenwinkelsatzes; gilt da Kontraposition immer Äquivalent zum ursprünglichen Satz
4.) Äquivalenz des Stufenwinkelsatzes; gilt erst wenn die Umkehrung bewiesen wurde --Wüstenfuchs 12:44, 4. Jul. 2013 (CEST)

Das hat nichts mit gelten oder nicht gelten zu tun. 2) und 4) sind Sätze, die beweisbar sind und damit ebenfalls gelten.
   
Allerdings sind beide keine äquivalenten Aussagen zum Stufenwinkelsatz, auch dann nicht, wenn ich sie bewiesen habe.--Tutorin Anne 14:05, 8. Jul. 2013 (CEST)