Lösung von Aufgabe 8.4P (SoSe 22)
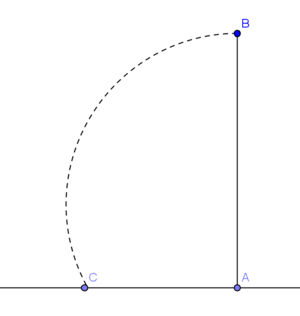
Auf einem neu anzulegenden Abenteuerspielplatz steht ein senkrecht nach oben ragender Baum (Strecke  ). Dieser soll an einer Stelle K so angesägt werden, dass er hier umknickt und mit seiner Spitze an einer Stelle C am Boden zu liegen kommt (siehe Skizze). Konstruieren Sie die Knickstelle K.
). Dieser soll an einer Stelle K so angesägt werden, dass er hier umknickt und mit seiner Spitze an einer Stelle C am Boden zu liegen kommt (siehe Skizze). Konstruieren Sie die Knickstelle K.
1. Schritt: Spiegelung des Punktes C an Strecke AB zu C`
2. Schritt: Verbindung von C zu B zu Strecke CB und Verbindung von C` zu B zu Strecke C`B, da C´ der Spiegelpunkt von C ist und laut der Längentreue die Strecke C`A die gleiche Länge besitzt wie CA, ist folglich die Stecke C`B gleichlang wie CB, daraus folgt, dass ich ein gleichschenkliges Dreieck erhalte aus CC`B
3. Schritt: da ein gleichschenkliges Dreieck einen Umkreis besitzt, brauch ich den Kreismittelpunkt von diesem Dreieck, diesen erhalte ich durch die Konstruktion der Mittelsenkrechten von Strecke CB und der Strecke C`B, welche beide die Strecke AB in einem Punkt S schneiden. Dieser Punkt S ist der Kreismittelpunkt, die Strecken SB, SC und SC` sind jeweils gleichlang und gleichzeitig der Radius des Kreises. Daraus folgt, dass der Punkt S genau die Stelle sein muss, an welchem der Baum angesägt wird, um auf Punkt C mit der Spitze zum liegen zu kommen, da der Punkt C auf dem Umkreis des Dreiecks CC`B liegt und B nur dann dort landet, wenn es dieselbe Streckenlänge ist von S zu C wie von S zu B--Kwd077 (Diskussion) 13:54, 14. Jun. 2022 (CEST)
Eine richtige Lösung. Aufgrund des Mittelsenkrechtenkriteriums benötigst du aber nicht die lange Begründung über das gleichschenklige Dreieck.--Matze2000 (Diskussion) 16:31, 16. Jun. 2022 (CEST)