Lösung von Aufgabe 9.1P (WS 13/14)
Aus Geometrie-Wiki
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
- (1) Def.:
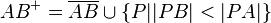
- (1) Def.:
- (2)
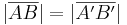 ; Streckentreue der Geradenspiegelung
; Streckentreue der Geradenspiegelung
- (2)
- (3)
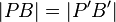 und
und 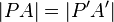 ; Streckentreue der Geradenspiegelung
; Streckentreue der Geradenspiegelung
- (3)
- (4)
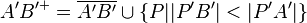 ; (1);(2);(3);
; (1);(2);(3);
- (4)
- --EarlHickey (Diskussion) 21:34, 9. Feb. 2014 (CET)
Ich kann den Beweis nachvollziehen. Allerdings stimmt die Definition für die Halbgerade nicht und damit ist der Beweis zwar eine guter Anhaltspunkt für den korrekten Beweis, aber so nicht richtig. --Tutorin Anne (Diskussion) 13:35, 10. Feb. 2014 (CET)

