Lösung von Zusatzaufgabe 5.2 P (SoSe 12)
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden 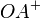 und
und 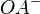 :
:
a)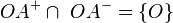 und
und
b)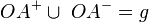
a)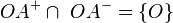
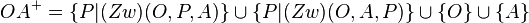
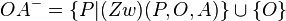
in der schnittmenge gibt es nur ein gemeinsames element: "o"
- es ist noch zu beweisen, dass keine weiteren Punkte außer O in der Schnittmenge liegen. Dies lässt sich am einfachsten indirekt beweisen.--Tutorin Anne 17:13, 27. Mai 2012 (CEST)
muss es noch bewiesen werden? wir wissen doch, dass alle drei zwischenrelationen disjunkt sind...--Studentin 17:58, 27. Mai 2012 (CEST)
- das ist richtig - dies kann für den Beweis auch genutzt werden. Trotzdem sollte man noch beweisen, dass jegliche Kombinationen nicht möglich sind. Diese muss man getrennt nennen und dann begründen, warum sie nicht möglich sind.--Tutorin Anne 16:32, 28. Mai 2012 (CEST)
b)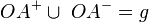
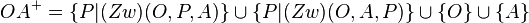
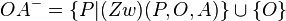
in der vereinigungsmenge ist die gerade g, da in der vereinigungsmenge sowohl die punkte a und o, als auch alle punkte zw (a,o,p), zw (p,o,a), zw (o,p,a) enthalten sind.
--Studentin 16:35, 27. Mai 2012 (CEST)
Ich habe es auch wie oben versucht zu beweisen. Doch wie baue ich den Beweis denn richtig auf? Ich brauche ja zwei Fälle, einmal den Existenzbeweis und den Eindeutigkeitsbeweis. Ich weiß nicht wie ich das machen soll?
| Voraussetzung | (V. hier eintragen) |
| Behauptung | 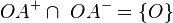
|
zu zeigen: 1. 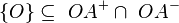
2. Es ist kein weiters Element in der Schnittmenge und damit 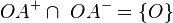
Beweis 1. Siehe oben bei Studentin.
Beweis 2. Ist hier noch zu führen:
Annahme: (hier ausfüllen)
Wisst ihr welche Kombinationen ich meine, von denen ich oben geschrieben habe?--Tutorin Anne 09:18, 12. Jun. 2012 (CEST)

