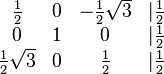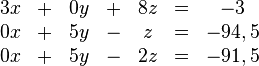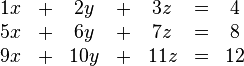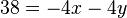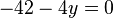Serie 3: LGS lösen SoSe 2018

Aufgabe 3.1 SoSe 2018 Lösen Sie das folgende Gleichungssystem: $\begin{pmatrix} \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Aufgabe 3.2 SoSe 2018 Lösen Sie das folgende Gleichungssystem: $\begin{pmatrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Aufgabe 3.3 SoSe 2018 Gegeben ist die große Koeffizientenmatrix eines lineraren Gleichungssystems: $\begin{matrix} \frac{1}{2} & 0 & -\frac{1}{2}\sqrt{3} & \vert \frac{1}{2} \\ 0 & 1 & 0 & \vert \frac{1}{2} \\ \frac{1}{2}\sqrt{3} & 0 & \frac{1}{2} & \vert \frac{1}{2} \end{matrix}$ Lösen Sie dieses Gleichungssystem. Aufgabe 3.4 SoSe 2018 Lösen Sie das folgende LGS: $\begin{matrix} 3x &+& 0y &+& 8z &=& -3 \\ 0x &+& 5y &-& z &=& -94,5 \\ 0x &+& 5y &-& 2z &=& -91,5 \end{matrix}$ Aufgabe 3.5 SoSe 2018 Lösen Sie das folgende LGS: $\begin{matrix} 1x &+& 2y &+& 3z &=& 4 \\ 5x &+& 6y &+& 7z &=& 8 \\ 9x &+& 10y &+& 11z &=& 12 \end{matrix}$ Aufgabe 3.6 SoSe 2018 Lösen Sie das folgende LGS: $38 = -4x - 4y$ $-42 - 4y = 0$ Aufgabe 3.7 SoSe 2018 Geben Sie ein LGS mit zwei Gleichungen und zwei Unbekannten an, dessen Lösungsmenge sich als Gerade interpretieren lässt. Aufgabe 3.8 SoSe 2018 Geben Sie ein LGS mit 3 Gleichungen und 3 Unbekannten an, dessen Lösungsmenge sich als Gerade interpretieren lässt. Aufgabe 3.9 SoSe 2018 Geben Sie ein LGS mit 3 Gleichungen und 3 Unbekannten an, dessen Lösungsmenge sich als Ebene interpretieren lässt. Aufgabe 3.10 Geben Sie ein LGS mit 3 Gleichungen und 3 Unbekannten an, dessen Lösungsmenge die leere Menge ist.
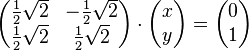
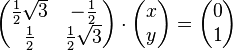