Übung 11 SoSe 12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 11.4) |
|||
| Zeile 19: | Zeile 19: | ||
== Aufgabe 11.4 == | == Aufgabe 11.4 == | ||
| − | + | Beweisen Sie: Sei <math>\overline{ABC} </math> ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:<br /> | |
| + | <math>\left| \alpha \right| > \left| \beta \right| \Rightarrow \left| a \right| > \left| b \right|</math> | ||
| + | |||
<br /> | <br /> | ||
[[Lösung von Aufg. 11.4_S]] | [[Lösung von Aufg. 11.4_S]] | ||
| − | == Aufgabe 11. | + | == Aufgabe 11.4 == |
| − | + | Definieren Sie: Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel. | |
<br /> | <br /> | ||
| − | [[Lösung von Aufg. 11. | + | [[Lösung von Aufg. 11.4_S]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Version vom 5. Juli 2012, 10:54 Uhr
Inhaltsverzeichnis |
Aufgabe 11.1
Definieren Sie die Begriffe Innenwinkel eines Dreiecks und Außenwinkel eines Dreiecks.
Aufgabe 11.2
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Aufgabe 11.3
Beweisen Sie:
Korollar 2 zum schwachen Außenwinkelsatz
- Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Aufgabe 11.4
Beweisen Sie: Sei  ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:
ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:
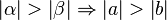
Aufgabe 11.4
Definieren Sie: Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel.
Lösung von Aufg. 11.4_S

