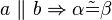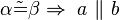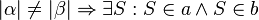Übung Aufgaben 4 (SoSe 18): Unterschied zwischen den Versionen
(→Aufgabe 4.1) |
|||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
==Aufgabe 4.1== | ==Aufgabe 4.1== | ||
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | ||
| − | + | a) Wie lautet die Umkehrung des Basiswinkelsatzes?<br /> | |
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen. | b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen. | ||
<br /> | <br /> | ||
| − | + | Vielen Dank für die umfangreichen Lösungen :-). Bitte aber die Lösungen jeweils auf die Lösungsseite stellen (nachfolgenden Link anklicken!). Ich habe mal alles entsprechend kopiert.--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 10:38, 9. Mai 2018 (CEST) | |
| + | |||
[[Lösung von Aufgabe 4.1 (SoSe_18)]] <br /> | [[Lösung von Aufgabe 4.1 (SoSe_18)]] <br /> | ||
| − | |||
| − | |||
==Aufgabe 4.2== | ==Aufgabe 4.2== | ||
| Zeile 28: | Zeile 27: | ||
b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br /> | b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br /> | ||
| − | [[Lösung von Aufgabe 4.2 (SoSe_18)]] | + | [[Lösung von Aufgabe 4.2 (SoSe_18)]] <br /> |
==Aufgabe 4.3== | ==Aufgabe 4.3== | ||
| Zeile 37: | Zeile 36: | ||
#<math>\left|\alpha \right|\not= \left| \beta \right| \Rightarrow \exists S: S \in a \wedge S \in b </math> | #<math>\left|\alpha \right|\not= \left| \beta \right| \Rightarrow \exists S: S \in a \wedge S \in b </math> | ||
#<math>\ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | #<math>\ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | ||
| − | [[Lösung von Aufgabe 4.3 (SoSe_18)]] | + | [[Lösung von Aufgabe 4.3 (SoSe_18)]] <br /> |
==Aufgabe 4.4== | ==Aufgabe 4.4== | ||
| Zeile 43: | Zeile 42: | ||
a) Wie lautet die Kontraposition dieser Implikation?<br /> | a) Wie lautet die Kontraposition dieser Implikation?<br /> | ||
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | ||
| − | [[Lösung von Aufgabe 4.4 (SoSe_18)]] | + | [[Lösung von Aufgabe 4.4 (SoSe_18)]] <br /> |
| + | |||
| + | |||
==Aufgabe 4.5== | ==Aufgabe 4.5== | ||
| Zeile 52: | Zeile 53: | ||
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.<br /> | Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.<br /> | ||
| − | [[Lösung von Aufgabe 4.5 (SoSe_18)]] | + | [[Lösung von Aufgabe 4.5 (SoSe_18)]] < br/> |
| + | |||
| + | |||
[[Category:Geo_P]] | [[Category:Geo_P]] | ||
Aktuelle Version vom 9. Mai 2018, 10:39 Uhr
Inhaltsverzeichnis |
Aufgaben zu Sätzen und Beweisen
Aufgabe 4.1
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
a) Wie lautet die Umkehrung des Basiswinkelsatzes?
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen.
Vielen Dank für die umfangreichen Lösungen :-). Bitte aber die Lösungen jeweils auf die Lösungsseite stellen (nachfolgenden Link anklicken!). Ich habe mal alles entsprechend kopiert.--Schnirch (Diskussion) 10:38, 9. Mai 2018 (CEST)
Lösung von Aufgabe 4.1 (SoSe_18)
Aufgabe 4.2
Satz: In einem Dreieck 
mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.
Beweis 2)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch.
Lösung von Aufgabe 4.2 (SoSe_18)
Aufgabe 4.3
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel 
und 
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
Lösung von Aufgabe 4.3 (SoSe_18)
Aufgabe 4.4
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 4.4 (SoSe_18)
Aufgabe 4.5
Vergleichen Sie die Wahrheitswerte von
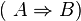und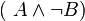 
.
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
