Der Inkreis und die Winkelhalbierenden eines Dreiecks (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Satz XV.3 : (Existenz und Eindeutigkeit des Inkreises)) |
(→Winkelhalbierendenkriterium) |
||
| Zeile 11: | Zeile 11: | ||
(auch das sollten Sie jetzt selbst hinbekommen:)<br /><br /> | (auch das sollten Sie jetzt selbst hinbekommen:)<br /><br /> | ||
| − | <br />Der Strahl <math>\ SW^{+}</math> ist genau dann Winkelhalbierende des Winkels <math>\angle ASB</math> , wenn | + | <br />Der Strahl <math>\ SW^{+}</math> ist genau dann Winkelhalbierende des Winkels <math>\angle ASB</math> , wenn jeder Punkt der Winkelhalbierenden zu den Schenkeln ein und denselben Abstand hat. --[[Benutzer:Teufelchen|Teufelchen]] 23:24, 11. Jul. 2011 (CEST)<br /><br /> |
===== Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks) ===== | ===== Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks) ===== | ||
Version vom 12. Juli 2011, 00:21 Uhr
Inhaltsverzeichnis |
Winkelhalbierenden eines Dreiecks
Definition XV.1 : (Winkelhalbierenden eines Dreiecks)
- Unter den Winkelhalbierenden eines Dreiecks versteht man die Winkelhalbierenden der Innenwinkel des Dreiecks.
Satz XV.1a : (Abstand eines Punktes einer Winkelhalbierenden zu den Schenkeln des Winkels)
- Jeder Punkt der Winkelhalbierenden eines Winkels hat zu den Schenkeln des Winkels jeweils ein und denselben Abstand.
Satz XV.1b : (Umkehrung von Satz XV.1a)
(das können Sie selbst:)
Winkelhalbierendenkriterium
(auch das sollten Sie jetzt selbst hinbekommen:)
Der Strahl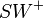 
ist genau dann Winkelhalbierende des Winkels 
, wenn jeder Punkt der Winkelhalbierenden zu den Schenkeln ein und denselben Abstand hat. --Teufelchen 23:24, 11. Jul. 2011 (CEST)
Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks)
Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.
Beweis von Satz XV.2 mit Hilfe des Winkelhalbierendenkriteriums: Versuchen Sie es selbst:
Inkreis eines Dreiecks
Definition XV.2 : (Tangente an einen Kreis)
Eine Gerade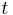 
berührt einen Kreis 
, wenn sie mit dem Kreis genau einen Punkt 
gemeinsam hat. Die Gerade 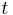heißt Tangente im Punkt .
Definition XV.3 : (Strecke berührt Kreis)
Eine Strecke 
berührt einen Kreis , wenn sie... (ergänzen Sie!)
Definition XV.4 : (Inkreis eines Dreiecks)
- Ein Kreis, der alle drei Seiten eines Dreiecks in jeweils genau einem Punkt berührt, heißt Inkreis des Dreiecks.
Satz XV.3 : (Existenz und Eindeutigkeit des Inkreises)
...ergänzen Sie!
Jedes Dreieck hat genau einen Inkreis.--Teufelchen 23:26, 11. Jul. 2011 (CEST)
