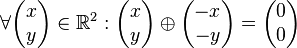Die abelsche Gruppe der geordneten Tripel reeller Zahlen 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> {|width=90%| style="background…“)
 
(→‎Abgeschlossenheit der additiven Verknüpfung \oplusauf \mathbb{R}^2)
Zeile 9: Zeile 9:
 
<math>\forall \begin{pmatrix} x_1  \\ y_1 \\ z_1 \end{pmatrix}, \begin{pmatrix} x_2  \\ y_2 \\ z_2 \end{pmatrix} \in \mathbb{R}^3: \begin{pmatrix} x_1  \\ y_1 \\z_1 \end{pmatrix} \oplus \begin{pmatrix} x_2  \\ y_2 \\ z_2\end{pmatrix}= \begin{pmatrix} x_1+x_2  \\ y_1+y_2 \\ z_1 + z_2\end{pmatrix}\</math>
 
<math>\forall \begin{pmatrix} x_1  \\ y_1 \\ z_1 \end{pmatrix}, \begin{pmatrix} x_2  \\ y_2 \\ z_2 \end{pmatrix} \in \mathbb{R}^3: \begin{pmatrix} x_1  \\ y_1 \\z_1 \end{pmatrix} \oplus \begin{pmatrix} x_2  \\ y_2 \\ z_2\end{pmatrix}= \begin{pmatrix} x_1+x_2  \\ y_1+y_2 \\ z_1 + z_2\end{pmatrix}\</math>
  
−
=Abgeschlossenheit der additiven Verknüpfung <math>\oplus</math>auf <math>\mathbb{R}^2</math>=
+
=Abgeschlossenheit der additiven Verknüpfung <math>\oplus</math>auf <math>\mathbb{R}^3</math>=
 
Folgt unmittelbar aus der Abgeschlossenheit der Addition auf <math>\mathbb{R}</math>
 
Folgt unmittelbar aus der Abgeschlossenheit der Addition auf <math>\mathbb{R}</math>
 +
 
=Die Assoziativität von <math>\oplus</math> auf <math>\mathbb{R}</math>=
 
=Die Assoziativität von <math>\oplus</math> auf <math>\mathbb{R}</math>=
 
... Ergänzen Sie selbst.
 
... Ergänzen Sie selbst.

Version vom 12. Dezember 2012, 19:20 Uhr

Inhaltsverzeichnis

Die nichtleere Menge

\mathbb{R}^3:=\mathbb{R} \times \mathbb{R} \times \mathbb{R}

Die additive Verknüpfung

Fehler beim Parsen(Lexikalischer Fehler): \forall \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix}, \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \in \mathbb{R}^3: \begin{pmatrix} x_1 \\ y_1 \\z_1 \end{pmatrix} \oplus \begin{pmatrix} x_2 \\ y_2 \\ z_2\end{pmatrix}= \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \\ z_1 + z_2\end{pmatrix}\


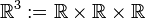
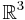
Abgeschlossenheit der additiven Verknüpfung \oplusauf \mathbb{R}^3

Folgt unmittelbar aus der Abgeschlossenheit der Addition auf \mathbb{R}

Die Assoziativität von \oplus auf \mathbb{R}

... Ergänzen Sie selbst.

Das neutrale Element bzgl. \oplus

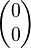\begin{pmatrix} 0 \\ 0 \end{pmatrix} leistet das Verlangte. (Überzeugen Sie sich davon.)

Die Inversen Elemente bzgl. \oplus

\forall \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2: \begin{pmatrix} x \\y \end{pmatrix} \oplus \begin{pmatrix} -x \\-y \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}

Kommutativität von \oplus

Folgt unmittelbar aus der Kommutativität der Addition reeller Zahlen.

Von „http://geometrie.zum.de/index.php?title=Die_abelsche_Gruppe_der_geordneten_Tripel_reeller_Zahlen_2012_13&oldid=19602“