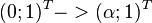GeometrieUndUnterrichtSS2019 04
Inhaltsverzeichnis |
Vorbereitungsauftrag
Vom Volumen zum Flächeninhalt
Denken Sie sich einen mit rechtiger Innenquerschnittsfläche (Würfel, Milchkarton,…). Gesucht ist der Flächeninhalt der Innenquerschnittsfläche (Grundfläche). Zur Verfügung stehen Ihnen Wasser, eine Waage und ein Maßband.
- Wie würden Sie mit Hilfe der gegebenen Hilfsmittel den gesuchten Flächeninhalt bestimmen?
- Übertragen Sie ihr vorgehen auf Körper mit zylinder-förmiger Innenquerschnittsfläche (Tasse, Regentonne, Mülleimer,…) und auf allgemeine Zylinder.
- In dieser Aufgabe wurde das Problem der Flächenmessung auf das Problem der Volumenmessung zurückgeführt. Aus sicht der gewöhnlichen Sequenzierung der mathematischen Inhalte in der Sekundarstufe erscheint dieses Vorgehen zunächst fragwürdig. Erläutern Sie, warum das Problem der Volumenmessung im Alltag tatsächlich das einfacherere Problem ist.
Vom Flächeninhalt zum Volumen
Lesen Sie den Abschnitt „Prinzip von Cavalieri, Satz von Dehn und Pyramidenvolumen“ aus dem Skript zur „Didaktik der Mathematik in der Sek. I“, Kapitel „Didaktik der Geometrie“, von Prof. Dr. Jürgen Roth (Universität Koblenz Landau).
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit dem Satz von Cavalieri nach.
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit Stufenkörpern nach.
- Für welchen Unterrichtsgang würden Sie sich in Ihrem Unterricht entscheiden? Warum?
Vorbereitungsauftrag (Zusatz)
Der Satz von Fubini ist ein Satz über die Möglichkeit der Berechnung von Doppelintegralen durch iterative Integration:
Bearbeiten Sie die folgenden Aufträge.
- Wiederholen Sie den Satz von Fubini aus Ihrer entsprechenden Mathematik-Vorlesung (vermutlich Analysis, Maßtheorie, Wahrscheinlichkeitstheorie, Funkionalanalysis o.Ä.).
- Formulieren Sie den Satz von Fubini für folgenden Spezialfall: Es sei
 ein abgeschlossener Quader, und
ein abgeschlossener Quader, und  ein abgeschlossenes Intervall. Ferner sei
ein abgeschlossenes Intervall. Ferner sei  messbar. Wir betrachten für
messbar. Wir betrachten für 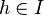 die Mengen
die Mengen 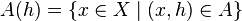 . Wie können Sie
. Wie können Sie 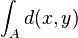 berechnen?
berechnen?
- Für das Prinzip von Cavalieri findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen.
- Welche Bestandteile der Schulbuch-üblichen Formulierung entsprechen welchen Bestandteilen der fachmathematisch präzisen Formulierung?
Das Prinzip von Cavalieri (für Körper)
Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben.
Sitzungsmaterialien
- Begleitfolien der Seminarsitzung vom 17.05.2019
- Vortragsnotizen für die Integration des Paralellograms
- Sie auch Zusatzmaterial Fläche und Volumen auf der Mathematischen Medienplattform des Mathematischen Instituts der Universität Heidelberg.
Dokumentation der Sitzung
Zusammenfassung
Diese Sitzung beschäftigte sich exemplarisch mit der Bestimmung des Flächeninhaltes von Parallelogrammen als Einstieg in den Themenkomplex "Messen".
Inhaltlicher Input (Einführung)
In den Bildungsstandards von Baden-Württemberg findet sich die Leitidee Messen. In diesem Zusammenhang ist oft auch von den vier Grundprinzipien des Messens die Rede:
- Vergleichsaspekt
- Messe-durch-Auslegen-und-Zählen-Aspekt
- Messgeräte-Aspekt
- Messen-als-Berechnen-Aspekt
[Details, siehe oben verlinkte Sitzungsfolien]
Da die Bestimmung von Flächeninhalt/Volumen als Integration angesehen werden kann [Propädeutik], haben wir uns in der folgenden Arbeitsphase mit der Berechnung des Flächeninhalts von Parallelogrammen [mithilfe der Integrationstheorie] beschäftigt.
Arbeitsphase (Flächeninhalt eines Parallelogramms)
Aufwärmübung - Flächeninhalt eines Rechtecks.
Sei 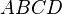 ein Rechteck mit Grundseite
ein Rechteck mit Grundseite  und Höhe
und Höhe  . Dieses Rechteck kann man wie folgt in einem 2D-Koordinatensystem betrachten:
Der Punkt
. Dieses Rechteck kann man wie folgt in einem 2D-Koordinatensystem betrachten:
Der Punkt  ist der Ursprung mit Koordinaten
ist der Ursprung mit Koordinaten 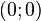 , der Punkt
, der Punkt  entspricht dem Punkt mit Koordinaten
entspricht dem Punkt mit Koordinaten 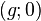 und der Punkt
und der Punkt  entspricht dem Punkt mit Koordinaten
entspricht dem Punkt mit Koordinaten 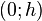 .
Dadurch ist auch bereits
.
Dadurch ist auch bereits  mit
mit 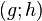 eindeutig festgelegt.
Nun kann die Berechnung des Flächeninhalts als Bestimmung der Fläche Zwischen x-Achse und der Geraden durch
eindeutig festgelegt.
Nun kann die Berechnung des Flächeninhalts als Bestimmung der Fläche Zwischen x-Achse und der Geraden durch  und
und  auf dem Intervall
auf dem Intervall ![[0, g]](/images/math/c/6/1/c61257efbb4f5b53f04b0c810d1b4922.png) betrachte werden. Es handelt sich also um eine simple Integration. Man erhält:
betrachte werden. Es handelt sich also um eine simple Integration. Man erhält:
![F_{ABCD} = \int_0^g h \, dt = [ht]^g_0 = hg](/images/math/0/d/b/0db0d22fade7c39f443679f55ecd0d43.png) .
.
Dieser Ansatz verwendet gerade die Rieman-Integration.
Natürlich wäre aber auch eine Integration über die Höhe  Mittels der Lebesgue-Integration möglich gewesen. Man erhält so:
Mittels der Lebesgue-Integration möglich gewesen. Man erhält so:
![F_{ABCD} = \int_0^h g \, dt = [gt]^h_0 = gh](/images/math/0/8/d/08ddf8e165f47ec21d78b4b75e816538.png) .
.
Flächeninhalt eines Parallelogramms
Im Folgenden werden nun verschiedene Ansätze zur Bestimmung des Flächeninhalts eines Parallelogramms  vorgestellt. Für die exakten Rechnungen sei auf die verlinkten Vortragsnotizen des Dozenten verwiesen.
vorgestellt. Für die exakten Rechnungen sei auf die verlinkten Vortragsnotizen des Dozenten verwiesen.
| Idee | Skizze | Ausführung | Entsprechung |
|---|---|---|---|
| Zerlege das Parallelogramm in drei Teile | Man berechnet 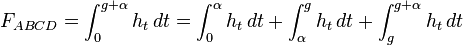 . . Zur Berechnung von |
Die Integration entlang der Grundseite (Riemann) entspricht gerade der Zerlegung des Parallelogramms in Rechteck und Dreiecke. | |
| Betrachte eine Parallele zur Grundseite und Integriere über die Höhe | Analog zum Rechteck. Es gilt: 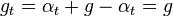 |
Die Integration entlang der Höhe (Lebesgue) entspricht der Idee, dass Scherungen Flächeninhalte nicht ändern. | |
| Mittels der Determinante bzw. Koordinatentransformation | siehe zum Beispiel hier | Die Transformation um Scherung  ist gegeben durch ist gegeben durch
|
Scherungen entsprechen Koordinatentransformationen |
Das Prinzip von Cavalieri (für Körper)
Im Raum werden zwei Körper und die Schar aller zu einer Ebene parallelen Ebenen betrachtet. Wenn für jede Ebene der Schar die beiden Schnittflächen mit den zwei Körpern gleichen Flächeninhalt haben, so sind die beiden Körper volumengleich.
Das Prinzip von Cavalieri (für Flächen)
In einer Ebene werden zwei Figuren und die Schar aller zu einer Geraden parallelen Geraden betrachtet. Wenn für jede Gerade der Schar die beiden Schnitte mit den zwei Figuren gleich lang sind, so sind die beiden Figuren flächengleich.
Nachbereitungsauftrag
Im Jahre 1994 veröffentlichte das Journal Diabetes Care den Artikel „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“ von Mary M. Tai. In dem Artikel entwickelt und validiert Tai eine Methode zur Berechnung der Fläche unter einer Blutzuckerkurve.
- Finden Sie heraus, wann und von wem die Integrationstheorie und insbesondere die Trapezregel entwickelt wurde. Lesen Sie dann Tai (1994) „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“.
- Für die Validierung „ihres“ Approximationsverfahrens vergleicht Tai ihre Rechenergebnisse mit einem Bestimmungsverfahren für den „wahren Wert“. Diskutieren Sie die beiden Verfahren vor dem Hintergrund des Messen-durch-Auslegen-und-Zählen-Aspekts, des Messen-als-Berechnen-Aspekts und des Vergleichsaspekt (vgl. Grundprinzipien des Messens in ).
- Analysieren Sie die Fehler/Fehlvorstellung zum Messen, die in dem Artikel sichtbar werden. Skizzieren Sie Hypothesen, wie diese Fehlvorstellungen entstanden sein könnten und wie Sie Ihnen im Unterricht der Sekundarstufe II begegnen bzw. im Unterricht der Sekundarstufe I vorbeugen könnten.
Ergebnisse der Nachbereitung
Tragen Sie hier die Ergebnisse Ihrer Nachbereitung in Textform (nicht länger als 500 Wörter) ein.
Abgabe von Max Mustermann
Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet.
Abgabe von pq
- Die Frage nach Flächeninhalten, hier speziell im Flächeninhalt unter einer Kurve aka Integral, ist so alt wie die Mathematik selbst. Die in der Arbeit Tai (1994) „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“ angeführte Methodik des Ausfüllens oder Erschöpfens einer Fläche durch kleinere Flächen, deren Flächeninhalte durch bekannte Formeln trivial bestimmbar sind, findet sich zuerst beim antiken griechischen Philosophen Antiphon, der im 5. Jahrhundert vor Christus lebte. Dieser Methode bediente sich später auch Johannes Kepler, der bei der Berechnung von Planetenbahnen eben Integrale durch einfachere Flächen approximierte und damit die heute bekannte numerische Integration nutzte. Basierend auf dieser einfachen Idee entwickelten die Mathematiker Gottfried Wilhelm Leibniz und Sir Isaac Newton unabhängig voneinander die Theorie der Differential- und Integralrechnung, welche mithilfe der Infinitesimalrechnung die Approximation eines Integrals durch infinitesimal kleine Quader oder Trapeze erlaubt. Numerische Verfahren zur Bestimmung solcher einfacher, aber auch komplexerer, Integrale waren 1994 sicher bereits weit verbreitet.
- Zur Validierung ihres Verfahrens vergleichen Tai et al. die Ergebnisse ihrer neuartigen Methode mit einer ground truth, welche darin besteht, die Kurve auf Millimeterpapier zu zeichnen und die Kästchen unter der Kurve zu zählen (Messen-durch-Auslegen-und-Zählen-Aspekt) (The validity of each model was verified through comparison of the total area obtained from the above formulas to a standard (true value), which is obtained by plotting the curve on graph paper and counting the number of small units under the curve. The sum of these units represents the actual total area under the curve.). Dabei scheinen sie nicht zu bemerken, dass dieses Verfahren ebenso eine Approximation des gewünschten Ergebnisses ist, wenn auch eine hinreichend genaue. Beide Verfahren beinhalten also einen Prozess des Messens. Die "neu entwicklete" Methode beinhaltet über das Messen der Seiten der Trapeze hinaus jedoch einige Rechnungen und entspricht vielmehr einem berechnenden Ansatz, wie es eben auch der Fall für das Berechnen von Flächeninhalten von einfachen geometrischen Objekten der Fall ist (Messen-als-Berechnen-Aspekt). Beide Methoden werden empirisch verglichen, indem man die relativen Abweichungen der Ergebnisse in verschiedenen Tests prüft. Dabei scheint den Autoren auch nicht bewusst zu sein, dass es sich bei ihrem Vergleich nicht um einen Beweis handelt, welcher ihre Methode validiert. Beispielsweise könnten die Tests nur einen Teil von möglichen Szenarien abdecken, in welchen ihr Verfahren eben die gewünschte Genauigkeit aufweist. Schließlich werden die Abweichungen der neuen Methode von der "ground truth" als "statistisch nicht signifikant" bezeichnet (?).
- Aus dem Artikel wird klar, dass die Autoren die reine Messmethode für die genauere Methode, welche das "echte Ergebnis" liefert, halten. Ihre berechnende Methode halten sie, zu Recht, für eine Approximation. Unklar bleibt, wie die tatsächlichen Kurven der Tests aussahen und welche Annahmen über diese Kurven getroffen wurden. Wurden die Kurven beispielsweise als stückweise linear angenommen, so liefert die angewandte Trapezregel offenbar sogar das exakte Ergebnis und ist damit sogar genauer als die Messen-durch-Auslegen-und-Zählen-Methode. Das Missverständnis der Autoren scheint für mich auf der kindlichen Vorstellung zu beruhen, dass etwas, dass ich tatsächlich messe und sehe, das echte und richtige Ergebnis ist. Dagegen scheinen Tai et al. jedoch erkannt zu haben, das sie das Integral der Kurve (wenn sie denn nicht stückweise linear angenommen wird) durch die Trapeze und damit Flächen unter stückweisen linearen Kurven nur approximieren. Im Falle, dass die Trapezregel tatsächlich die exakte Lösung darstellt, bleibt diese Auffassung für mich jedoch ein Rätsel. Um solchen Vorstellungen vorzubeugen, sollte im Laufe der Sekundarstufe I stark betont werden, dass eine Messung immer mit einer Messgenauigkeit und einem Messfehler zusammenhängen. Hier könnten Beispiele und Vergleiche von Messung und Berechnung schon am Beispiel von Dreiecken herangezogen werden. Am Beispiel des Kreises lässt sich dieser Sachverhalt noch deutlicher darstellen, da sich Kreise nie vollständig durch Dreiecke oder Vierecke auslegen lassen. In der Sekundarstufe II ist es wichtig bei der Einführung des Hauptsatzes der Integral- und Differenzialrechnung darauf wert zu legen, dass die Approximation durch Ober- und Untersummen (i.e. Quader) immer genauer wird, wenn die Zerlegungsintervalle kleiner werden und nur dann exakt ist, wenn die Teile unendlich klein sind. Das analytische Integral ist also tatsächlich die einzige exakte Lösung für beliebige Kurven.
Weitere Fragen/Anmerkungen:
- Habe ich etwas falsch verstanden?
- Beispielrechnung auf Seite zwei enthält einen Klammerfehler/Typo, das Ergebnis ist jedoch korrekt.
- Wie rechtfertigt sich die Annahme, dass der Blutzuckerspiegel stückweise linear approximiert werden kann?
- Was waren die anderen Formeln zur Berechnung des Blutzuckers?
- Gab es 1994 keinen Reviewingprocess für wissenschaftliche Arbeiten?
- Was haben die Autoren dieser Arbeit im Mathematikunterricht gemacht?
- Warum wurde dieses Paper 273 mal zitiert, davon 6 Zitationen im Jahr 2019?!
Literaturhinweise
- Greefrath et al. (2016) „Didaktik der Analysis“.
- Hoffmann (2018). „Konzeption von fachmathematischen Schnittstellenmodulen für Lehramtsstudierende am Beispiel ausgewählter Themen der höheren Analysis“. In khdm-Report (Masterarbeit).
- Kapitel 5 (Flächeninhalte in den Klassen 5 bis 10) in Krauter (2008). „Beiträge zur Methodik und Didaktik des Geometrieunterrichts in der Sekundarstufe 1 (Klassen 5 bis 10)“.
- siehe auch: übergreifende Literaturhinweise
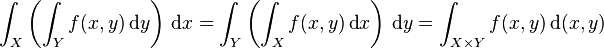

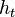 im ersten und dritten Summanden bietet sich ein Steigungsdreick zur Bestimmung von
im ersten und dritten Summanden bietet sich ein Steigungsdreick zur Bestimmung von  an.
an.

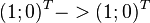 und
und