Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Restklassen modulo 4)
(→‎Restklassen modulo 4)
Zeile 15: Zeile 15:
 
#Die Verknüpfung <math>\oplus</math> ist auf der Menge <math>\mathbb{Z}_4</math> assoziativ, d.h. <math>\forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right)</math>,
 
#Die Verknüpfung <math>\oplus</math> ist auf der Menge <math>\mathbb{Z}_4</math> assoziativ, d.h. <math>\forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right)</math>,
 
#<math>\mathbb{Z}_4</math>  hat ein neutrales Element, nämlich die Klasse <math>\overline{0}</math>, d.h. <math> \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a}</math>,<br />
 
#<math>\mathbb{Z}_4</math>  hat ein neutrales Element, nämlich die Klasse <math>\overline{0}</math>, d.h. <math> \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a}</math>,<br />
−
#Zu jedem Element aus <math>\mathbb{Z}_4</math> gibt es ein inverses Element, d.h. <math>\forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} </math>
+
#Zu jedem Element aus <math>\mathbb{Z}_4</math> gibt es ein inverses Element, d.h. <math>\forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} </math>.
 +
 
 +
Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:
 +
 
 +
<ggb_applet width="155" height="176"  version="4.2" ggbBase64="UEsDBBQACAgIAGyQiUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAGyQiUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9u2Fv7c/QpC2LfrxKJIyXbhdGic9G5AOxRNNwz3GyUxNhdZ1JUoOxn24+8hKcpyFDtVu9XA7YLGJA/PC5+j80K5mf9wv87QhpeVkPmFh899D/E8kanIlxderW7Ppt4Pr76bL7lc8rhk6FaWa6YuPHoeeDs5WJ1TLSvSC+829qM0JekZprf8jEYTfhbHCT1LOPMnUzoL49vQQ+i+Ei9z+TNb86pgCb9JVnzN3sqEKaNypVTxcjzebrfnzvi5LJfj5TI+v69SD8HB8+rCayYvQd2e0JYY9sD38fi3d2+t+jORV4rlCfeQBlWLV9+9mG9Fnsot2opUrcAFUwC24mK5ApTBFE461kwFQC14osSGVyDaWRrMal14ho3lev+FnaGsheOhVGxEykvt5Nlk6ge4/fSQLAXPVcOKG5Njp2y+EXxrteqZMai9LyoRZxwczrIKEIn8tgRvtutKPWQ8ZmVL2J2GjAjsiz+AGRzkIesCMO37I/0bhP6I6o3xvlU4qpIyM0qBD6M/EQyBHQhCf5pJaNe0WUZ2OTED9u2Am82p/pjpRfSFiLBDRJ5CFPlPI6L+bHLEsCrrPbt2vTOLd2Zp12wwAyfiyWgCZsOwbxZ/EdjW5synA6B2Hp6PQuP0wA98NNIDtkMAQxTZLd/S4MGaIbADtUNoeagVp5aVWh5qeSjpoLSeOwzysWfbAMVh+OkY8ZdFEd4Z7TxMSAbzz/z2TJJBqdgLoM+wGNEvidjPMDjxv4bB+djVuXkTp6haad4mdBRfVzpyycwEL8IohAiNJhBrIcIzGCa6EgUIh4iGsMRTFOlxgoguPhQRNEWaDxNkQjScwgc1hSlCIejSxImtUIhQFBKETWBTBOGMTHJAogQEOMIQhSCkrWNtlkSIRrAgU0ThgDotJro+EpCDNRgPEMGIaFk8QUGEogBNdGphqjMumuqzg9IART6KtCjkFuSVzSmQmCKi0UCEF7ISrXNXPCvap2L8KPKiVo3vGnqyTp0flXzEnsrk7vKRszmrlJsDE/SiXcOzvWmvH76YZyzmGVwabnQcILRhmU5ho/9W5gq5GAgsbVmyYiWS6oYrBVIV+p1t2Fum+P0b4K7cAY1p06bnvE4ykQqW/wpBolVohch1bVMIXdeeTrC1kkhZpjcPFUQOuv8PLyUUZkzPZ90fqP4Pdos83gKVVcJ0zNPZ/s4UHsLDgb2Ztc03LTZ2zyvnzGVprkjW/XrxU3Upsx2pkCJXC1aoujRXMCiDpUb1Ol9m3DjX9H64zSR3sby/sV4lVtfHhwJWvj1AvFzITJYIUjLQJXTZjLEdDY8+WcvlGx7fcPjuMYm03cezwHCYMbaj4YLnbo/WIMUOJvadGVGZQgLKu1FmgkbfjepcqLduoURy1yDFlv/neh1DvDVi+yrxX6RyPn4UYfOqKDlLqxXn6smYM43JxRymU3swELpd8Cy76bLqAtreKRuvddSDi+t17jzUyATTY3y45SP+Mb7gE/nIzu7sGB/d8TUxVPFM1wGZI7S6SUqZZQbFpjNPjLyOGIhm/awaaBl7kLWuDfBA3sCLRZ2xy05f1uR/d/NFE360eh/z/fo0+RLMVbx8DzfpbG/DQvoREPJ9iQ9gwlBRS2ZZJrc3UO0Ey65ToWTb5czOR2hWH0XRpjj/bw1yH2AQJW/LLquVXMh1kXHFO+Vt388QN2/MCxZqXrTeMSjWwSgYxSMcvqQjaifBiNgJ3IbcVugolnmUjM4ICUMyI8COezS/UbFPo0/Qwh6NPqEvcGej7rSBOxJ1pyVugp9QQJwceWIT7yQDNwndhDq50E0sxaZ1L43nd7yEcLANIocSXcu6sh2r81jqir9navU6Tz/wJUT3e6avOwpqhmXdlaIUAmMNgpbeZDfT9foXqEGWmvJlyV3pyszbrK2YZtfvtqse2ah6U8r1T/nmIzSDR0edjx2eeZWUotA9B8Vw/7rju8xJRcXg9pZ25QB8BShs7iqhdHU0cbrSAQ4yTEfqDF3xP7gulnAFgvatW3HG1/C6ipRpN3m95qVI2tJ7GZg3YThk7XCcu9ID+YVk/DvUi93l20rt3An7B1oSpFuxYlof7rc4fQFYNmPT4hx/2+6g3gCMrm+N9XcybU6KncfhgRq3wNWhsAYRXHe4LbyqabOoAIWmS3fihtX3IhOsfNgPE2gv1mvP+m/R8x/+u/z3uf74it646nkj+Ia9cd3zBvmGvfGa/N9Vmq/pPfpPnel4I/ynznS8EX1bdSaR6zXLU5Sbb7TAtrf7HoX5F973rwn6F7r8Ht6mGNYvQRZlrRzDJbEqG0XPX5IOl65P8Z3/FyNbHEa2GIhs0UOGT4ns6jCyq4HIrnrIglMiuz6M7HogsuseMnIqZPSZPKMD8+xwkzsFsmN5NhDZoofsZNFIn8mzgciueshOGo3H8mwgsusespNV/fCZPAsH5tnh69MpkB3Ls4HIFj1kJ4vG8Jk8G4jsqofspNF4LM8GIrvuITtZ1Y+eybNoYJ4dvpifAtmxPBuIbNFDdrJojJ7Js4HIrnrIThqNx/JsILLrHrK/qeqPu99Vm/8Tbv4k7NX/AFBLBwiPska+jQcAAMEmAABQSwECFAAUAAgICABskIlB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAGyQiUGPska+jQcAAMEmAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAJAgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Version vom 9. Dezember 2012, 19:04 Uhr

Beispiele für endliche Gruppen

Restklassen modulo 4

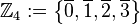
\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}
mit
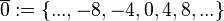\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\} (Menge aller durch 4 teilbaren ganzen Zahlen),
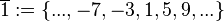\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
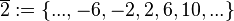\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
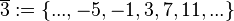\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),

Wir definieren auf \mathbb{Z}_4 eine Verknüpfung \oplus wie folgt:
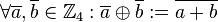
\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a}\oplus \overline{b} := \overline{a+b}

Die Struktur 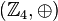\left(\mathbb{Z}_4, \oplus\right) ist eine Gruppe:

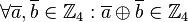  1. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 abgeschlossen, d.h. \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} \in \mathbb{Z}_4,
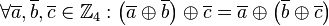  2. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 assoziativ, d.h. \forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right),
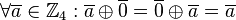  3. \mathbb{Z}_4 hat ein neutrales Element, nämlich die Klasse \overline{0}, d.h. \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a},
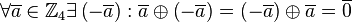  4. Zu jedem Element aus \mathbb{Z}_4 gibt es ein inverses Element, d.h. \forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} .

Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:

Von „http://geometrie.zum.de/index.php?title=Gruppen,_abelsche_Gruppen_2012_12&oldid=19390“