Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Restklassen modulo 4)
(→‎Restklassen modulo 4)
Zeile 21: Zeile 21:
 
<ggb_applet width="155" height="176"  version="4.2" ggbBase64="UEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9u2Fv7c/QpC2LfrxKJIyXbhdGic9G5AOxRNNwz3GyUxNhdZ1JUoOxn24+8hKcpyFDtVu9XA7YLGfDsvfA7PC+lm/sP9OkMbXlZC5hcePvc9xPNEpiJfXni1uj2bej+8+m6+5HLJ45KhW1mumbrw6Hng7fhgdE41r0gvvNvYj9KUpGeY3vIzGk34WRwn9CzhzJ9M6SyMb0MPoftKvMzlz2zNq4Il/CZZ8TV7KxOmjMiVUsXL8Xi73Z475eeyXI6Xy/j8vko9BBvPqwuv6bwEcXtMW2LIA9/H49/evbXiz0ReKZYn3EMaVC1effdivhV5KrdoK1K1AhNMAdiKi+UKUAZT2OlYExUAteCJEhteAWtnaDCrdeEZMpbr9Re2h7IWjodSsREpL7WRZ5OpH+D200OyFDxXDSluVI6dsPlG8K2VqntGoba+qESccTA4yypAJPLbEqzZjiv1kPGYle3EbjdkRGBd/AHEYCAPWROAat8f6d8g9EdUL4z3tcJWlZSZEQp0GP2JoAlsQxD603RCO6bNMLLDiWmwbxvcLE71x0wPoi9EhB0i8hSiyH8aEfVnkyOKVVnv6bXjnVq8U0u7aoMZGBFPRhNQG4Z9tfiLwLY6Zz4dALVzeD4KjdEDP/DRSDfYNgE0UWSXfDsHB2uawDbUNqGloZadWlJqaailoaSD0lpuyIk6kDgMPx0k/jI3wjulndOEaDD/zG9PJRkUiz0P+gyNEf0Sl/0MhRP/ayicj12imzeOiqqVpm18R/F1pV2XzIz3IoxCcNFoAs4WIjyDZqJTUYBwiGgIQzxFkW4niOjsQxFBU6TpMEHGR8MpfFCTmSIUgiw9ObEpChGKQoKw8WyKwJ+RiQ6IlIAARRiiEJi0dqzVkgjRCAZkiihsUMfFRCdIAnwwBuUBIhgRzYsnKIhQFKCJji1MdchFU713EBqgyEeRZoXggsCyQQUcU0Q0GvDwQlaiNe6KZ0V7KsaOIi9q1diumU/WqbOjko/IU5ncXT4yNmeVcn0ggmK0q3i2OO0VxBfzjMU8g1vDjfYDhDYs0yFs5N/KXCHnA4GdW5asWImkuuFKAVeFfmcb9pYpfv8GqCu3QaPa1Ok5r5NMpILlv4KTaBFaIHJl22RCV7anE2y1JFKW6c1DBZ6D7v/DSwmZGdPzWfcH0v+DXSKPl0BklTDt83S2vzKFQ3g4sDazuvmmxcbueeWMuSzNHcmaXw9+qi5ltpsqpMjVghWqLs0dDNJgqVG9zpcZN8Y1xR+uM8ldLO9vrFWJlfXxoYCRbzcQLxcykyWCkAx0Cl02bWxbQ6N31lL5hsY3FL47JpG263gWGArTxrY1VHDudmsNUuxgYt+pEZVJJCC862XGafTlqM6FeusGSiR3DVJs6X+u1zH4W8O2LxL/RSLn40ceNq+KkrO0WnGunvQ5U5icz+GoMQYw3S54lt10SXUCbS+VDWFHPJi4XufOQg1PMD1Gh1s64h+jCz6Rjuz0zo7R0R1d40MVz3QekDlCq5uklFlmUGw6/cTwa48Bb9Zn1UDL2IOsdW6AA3kDL4s6Y5eduqyn/92NFz3xo5X7mO7Xp6cvQV3Fy/dwlc72FiykHwEh3+f4ACrMLGqnWZbJ7Q1kO8Gy61Qo2VY5s/IRitVHUbQhzv9bA98HaETJ27TLaiUXcl1kXPFOetu3M/jNG/PCQs1L6x2DZB2MglE8wuFLOqK2E4yI7cBtyC2FbsYSj5LRGSFhSGYEyHFvzm9E7M/RJ+bC3hx9Ql7g9kbdbgO3Jep2S1wHPyGAOD7yxCLecQauE7oOdXyh69gZG9a9MJ7f8RLcwRaIHFJ0LevKVqzOsdQVf8/U6nWefuBL8O73TF93FOQMS7pLRSk4xhoY7XwT3Uzn618gB9nZlC9L7lJXZp6zNmOaVb9brnrTRtSbUq5/yjcfoRg82up87PDMq6QUha45KIb71x3fRU4qKga3t7TLB+ArQGFjVwmls6Px05V2cOBh2lNn6Ir/wXWyhCsQlG9dijO+hvcqUqbc5PWalyJpU+9lYJ7CsMna4Th3qQfiC8n4d8gXu8u35dqZE9YPlCQIt2LFtDzcL3H6ArBs2qbEOfq23EG+ARhd2xrt72Ta7BQ7i8OBGrPA1aGwChFcd7hNvKops6gAgaZKd/yG1fciE6x82HcTKC/Was/ab9GzH/677Pe59viK1rjqWSP4hq1x3bMG+Yat8Zr832War2k9+k+e6Vgj/CfPdKwRfVt5JpHrNctTlJtvtEC3t/sehfkX3vevCfoXuvweXlMM60eQRVkrR3BJrMhG0POXpMOp61Ns5//FyBaHkS0GIlv0kOFTIrs6jOxqILKrHrLglMiuDyO7HojsuoeMnAoZfSbO6MA4O1zkToHsWJwNRLboITuZN9Jn4mwgsqsespN647E4G4jsuofsZFk/fCbOwoFxdvj6dApkx+JsILJFD9nJvDF8Js4GIrvqITupNx6Ls4HIrnvITpb1o2fiLBoYZ4cv5qdAdizOBiJb9JCdzBujZ+JsILKrHrKTeuOxOBuI7LqH7G/K+uPud9Xm/4Sbvwl79T9QSwcIzlP2YogHAADCJgAAUEsBAhQAFAAICAgAsZCJQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACxkIlBzlP2YogHAADCJgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAB8IAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br />
 
<ggb_applet width="155" height="176"  version="4.2" ggbBase64="UEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9u2Fv7c/QpC2LfrxKJIyXbhdGic9G5AOxRNNwz3GyUxNhdZ1JUoOxn24+8hKcpyFDtVu9XA7YLGfDsvfA7PC+lm/sP9OkMbXlZC5hcePvc9xPNEpiJfXni1uj2bej+8+m6+5HLJ45KhW1mumbrw6Hng7fhgdE41r0gvvNvYj9KUpGeY3vIzGk34WRwn9CzhzJ9M6SyMb0MPoftKvMzlz2zNq4Il/CZZ8TV7KxOmjMiVUsXL8Xi73Z475eeyXI6Xy/j8vko9BBvPqwuv6bwEcXtMW2LIA9/H49/evbXiz0ReKZYn3EMaVC1effdivhV5KrdoK1K1AhNMAdiKi+UKUAZT2OlYExUAteCJEhteAWtnaDCrdeEZMpbr9Re2h7IWjodSsREpL7WRZ5OpH+D200OyFDxXDSluVI6dsPlG8K2VqntGoba+qESccTA4yypAJPLbEqzZjiv1kPGYle3EbjdkRGBd/AHEYCAPWROAat8f6d8g9EdUL4z3tcJWlZSZEQp0GP2JoAlsQxD603RCO6bNMLLDiWmwbxvcLE71x0wPoi9EhB0i8hSiyH8aEfVnkyOKVVnv6bXjnVq8U0u7aoMZGBFPRhNQG4Z9tfiLwLY6Zz4dALVzeD4KjdEDP/DRSDfYNgE0UWSXfDsHB2uawDbUNqGloZadWlJqaailoaSD0lpuyIk6kDgMPx0k/jI3wjulndOEaDD/zG9PJRkUiz0P+gyNEf0Sl/0MhRP/ayicj12imzeOiqqVpm18R/F1pV2XzIz3IoxCcNFoAs4WIjyDZqJTUYBwiGgIQzxFkW4niOjsQxFBU6TpMEHGR8MpfFCTmSIUgiw9ObEpChGKQoKw8WyKwJ+RiQ6IlIAARRiiEJi0dqzVkgjRCAZkiihsUMfFRCdIAnwwBuUBIhgRzYsnKIhQFKCJji1MdchFU713EBqgyEeRZoXggsCyQQUcU0Q0GvDwQlaiNe6KZ0V7KsaOIi9q1diumU/WqbOjko/IU5ncXT4yNmeVcn0ggmK0q3i2OO0VxBfzjMU8g1vDjfYDhDYs0yFs5N/KXCHnA4GdW5asWImkuuFKAVeFfmcb9pYpfv8GqCu3QaPa1Ok5r5NMpILlv4KTaBFaIHJl22RCV7anE2y1JFKW6c1DBZ6D7v/DSwmZGdPzWfcH0v+DXSKPl0BklTDt83S2vzKFQ3g4sDazuvmmxcbueeWMuSzNHcmaXw9+qi5ltpsqpMjVghWqLs0dDNJgqVG9zpcZN8Y1xR+uM8ldLO9vrFWJlfXxoYCRbzcQLxcykyWCkAx0Cl02bWxbQ6N31lL5hsY3FL47JpG263gWGArTxrY1VHDudmsNUuxgYt+pEZVJJCC862XGafTlqM6FeusGSiR3DVJs6X+u1zH4W8O2LxL/RSLn40ceNq+KkrO0WnGunvQ5U5icz+GoMQYw3S54lt10SXUCbS+VDWFHPJi4XufOQg1PMD1Gh1s64h+jCz6Rjuz0zo7R0R1d40MVz3QekDlCq5uklFlmUGw6/cTwa48Bb9Zn1UDL2IOsdW6AA3kDL4s6Y5eduqyn/92NFz3xo5X7mO7Xp6cvQV3Fy/dwlc72FiykHwEh3+f4ACrMLGqnWZbJ7Q1kO8Gy61Qo2VY5s/IRitVHUbQhzv9bA98HaETJ27TLaiUXcl1kXPFOetu3M/jNG/PCQs1L6x2DZB2MglE8wuFLOqK2E4yI7cBtyC2FbsYSj5LRGSFhSGYEyHFvzm9E7M/RJ+bC3hx9Ql7g9kbdbgO3Jep2S1wHPyGAOD7yxCLecQauE7oOdXyh69gZG9a9MJ7f8RLcwRaIHFJ0LevKVqzOsdQVf8/U6nWefuBL8O73TF93FOQMS7pLRSk4xhoY7XwT3Uzn618gB9nZlC9L7lJXZp6zNmOaVb9brnrTRtSbUq5/yjcfoRg82up87PDMq6QUha45KIb71x3fRU4qKga3t7TLB+ArQGFjVwmls6Px05V2cOBh2lNn6Ir/wXWyhCsQlG9dijO+hvcqUqbc5PWalyJpU+9lYJ7CsMna4Th3qQfiC8n4d8gXu8u35dqZE9YPlCQIt2LFtDzcL3H6ArBs2qbEOfq23EG+ARhd2xrt72Ta7BQ7i8OBGrPA1aGwChFcd7hNvKops6gAgaZKd/yG1fciE6x82HcTKC/Was/ab9GzH/677Pe59viK1rjqWSP4hq1x3bMG+Yat8Zr832War2k9+k+e6Vgj/CfPdKwRfVt5JpHrNctTlJtvtEC3t/sehfkX3vevCfoXuvweXlMM60eQRVkrR3BJrMhG0POXpMOp61Ns5//FyBaHkS0GIlv0kOFTIrs6jOxqILKrHrLglMiuDyO7HojsuoeMnAoZfSbO6MA4O1zkToHsWJwNRLboITuZN9Jn4mwgsqsespN647E4G4jsuofsZFk/fCbOwoFxdvj6dApkx+JsILJFD9nJvDF8Js4GIrvqITupNx6Ls4HIrnvITpb1o2fiLBoYZ4cv5qdAdizOBiJb9JCdzBujZ+JsILKrHrKTeuOxOBuI7LqH7G/K+uPud9Xm/4Sbvwl79T9QSwcIzlP2YogHAADCJgAAUEsBAhQAFAAICAgAsZCJQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACxkIlBzlP2YogHAADCJgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAB8IAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br />
 
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.
 
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.
 +
 +
Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe <math>\left(\mathbb{Z}_4, \oplus\right)</math>:<br />
 +
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung <math>\oplus</math> auf <math>\mathbb{Z}_4</math> kommutativ ist:<br />
 +
*<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.

Version vom 9. Dezember 2012, 19:13 Uhr

Beispiele für endliche Gruppen

Restklassen modulo 4

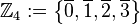
\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}
mit
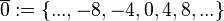\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\} (Menge aller durch 4 teilbaren ganzen Zahlen),
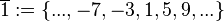\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
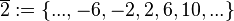\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
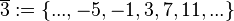\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),

Wir definieren auf \mathbb{Z}_4 eine Verknüpfung \oplus wie folgt:
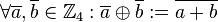
\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a}\oplus \overline{b} := \overline{a+b}

Die Struktur 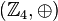\left(\mathbb{Z}_4, \oplus\right) ist eine Gruppe:

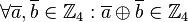  1. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 abgeschlossen, d.h. \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} \in \mathbb{Z}_4,
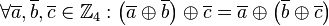  2. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 assoziativ, d.h. \forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right),
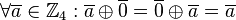  3. \mathbb{Z}_4 hat ein neutrales Element, nämlich die Klasse \overline{0}, d.h. \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a},
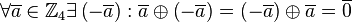  4. Zu jedem Element aus \mathbb{Z}_4 gibt es ein inverses Element, d.h. \forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} .

Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:



Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.

Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe 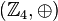\left(\mathbb{Z}_4, \oplus\right):
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung \oplus auf \mathbb{Z}_4 kommutativ ist:

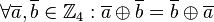  • \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}.
Von „http://geometrie.zum.de/index.php?title=Gruppen,_abelsche_Gruppen_2012_12&oldid=19393“