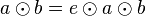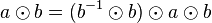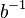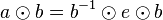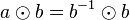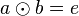Gruppendefinition (kurz): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#CCFFCC; padding:1em" | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| − | + | =Linksinvers gleich Rechtsinvers= | |
| − | + | ==Satz 1== | |
| − | + | Es sei <math>[G, \odot]</math> eine Gruppe.<br /> | |
| + | <math>\forall a \in G: a \odot b = e \land c \odot a = e \Rightarrow b=c</math> | ||
| + | ==Beweis von Satz 1== | ||
| + | Es sei <math>b</math> das Linksinverse bzgl. <math>\odot</math> von <math>a</math>. <br /> | ||
| + | Wir multiplizieren <math>b</math> von rechts mit <math>a</math>: | ||
| + | {| | ||
| + | |- | ||
| + | | (I)|| <math>a \odot b = e \odot a \odot b </math>|| (Wir haben <math>a</math> mit <math>b</math> von rechts multipliziert | ||
| + | |- | ||
| + | | (II) || <math>a \odot b = (b^{-1} \odot b)\odot a \odot b </math> ||(Auch <math>b</math> hat ein Linksinverses <math>b^{-1}</math> | ||
| + | |- | ||
| + | |(III) || <math>a \odot b = b^{-1} \odot (b\odot a) \odot b </math> || (Assoziativität) | ||
| + | |- | ||
| + | |(IV) || <math>a \odot b = b^{-1} \odot e \odot b </math> || (<math>b</math> ist das Linksinverse von <math>a</math>) | ||
| + | |- | ||
| + | | (V) || <math>a \odot b = b^{-1} \odot b </math> || (Eigenschaften des Einselements) | ||
| + | |- | ||
| + | | (VI) || <math>a \odot b = e </math> || (<math>b^{-1}</math> ist das Linksinverse von <math>b</math> | ||
| + | |} | ||
| + | Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von <math>a</math> auch Rechtsinverses von <math>a</math> ist. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 5. November 2017, 18:52 Uhr
Linksinvers gleich RechtsinversSatz 1Es sei Beweis von Satz 1Es sei
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe.
eine Gruppe.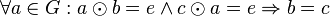
 das Linksinverse bzgl.
das Linksinverse bzgl.  von
von  .
.