Innenwinkelsatz für Dreiecke und starker Außenwinkelsatz (WS10/11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: == "Der Abreißbeweis" == Diskutieren Sie Sinn und Unsinn des folgenden "Beweises": http://www.ph-heidelberg.de/wp/gieding/Lehre/didaktik_5_8/flash/innenwinkelsumme.sw...) |
|||
| Zeile 17: | Zeile 17: | ||
===== Beweis von Satz XII.5: (Starker Außenwinkelsatz) ===== | ===== Beweis von Satz XII.5: (Starker Außenwinkelsatz) ===== | ||
Übungsaufgabe | Übungsaufgabe | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Version vom 23. Januar 2011, 20:46 Uhr
Inhaltsverzeichnis |
"Der Abreißbeweis"
Diskutieren Sie Sinn und Unsinn des folgenden "Beweises":
http://www.ph-heidelberg.de/wp/gieding/Lehre/didaktik_5_8/flash/innenwinkelsumme.swf
Ein echter Beweis
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 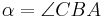 ,
, 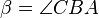 und
und 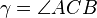 .
.
Es gilt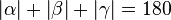 .
.
- Es sei
Beweis von Satz XII.4 (Innenwinkelsatz für Dreiecke)
Übungsaufgabe
Satz XII.5: (Starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der größen der beiden nicht anliegenden Innenwinkel dieses Dreiecks.
Beweis von Satz XII.5: (Starker Außenwinkelsatz)
Übungsaufgabe

