Lösung von Aufg. 7.2 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt g…“) |
Wookie (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \epsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält. | Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \epsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält. | ||
| + | '''Voraussetzung''': Gerade g, Punkt P: P <math> \notin</math> g <br /> | ||
| + | '''Behauptung''': <math> \exists!</math> Ebene E: g <math>\in</math> E <math>\wedge</math> P <math>\in</math> E <br /> | ||
| + | |||
| + | '''Beweis:''' <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1) P <math> \notin</math> g|| Vor. | ||
| + | |- | ||
| + | | 2) <math>\exists</math> R, Q <math>\in</math> g, R<math>\neq</math> Q || Axiom I/2 | ||
| + | |- | ||
| + | | 3) nkoll(P, Q, R) || Axiom I/3, 1), 2) | ||
| + | |- | ||
| + | | 4) <math> \exists!</math> E: (P, Q, R)<math>\in</math> E || Axiom I/4, 3) | ||
| + | |- | ||
| + | | 5) P <math> \in</math> E <math>\wedge</math> g <math>\subseteq</math> E || 4) | ||
| + | |} q.e.d. --[[Benutzer:Wookie|Wookie]] 14:16, 28. Nov. 2011 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 28. November 2011, 15:16 Uhr
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Voraussetzung: Gerade g, Punkt P: P 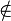 g
g
Behauptung: 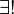 Ebene E: g
Ebene E: g  E
E  P
P  E
E
Beweis:
1) P 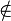 g g |
Vor. |
2)  R, Q R, Q  g, R g, R Q Q |
Axiom I/2 |
| 3) nkoll(P, Q, R) | Axiom I/3, 1), 2) |
4) 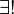 E: (P, Q, R) E: (P, Q, R) E E |
Axiom I/4, 3) |
5) P  E E  g g 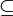 E E |
4) |

