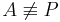Lösung von Aufg. 7.4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 5: | Zeile 5: | ||
<u>Fall 1:</u><br /> | <u>Fall 1:</u><br /> | ||
| − | 3 der vier Punkte liegen in der Ebene <math>\epsilon</math> trivial<br /> | + | 3 der vier Punkte liegen in der Ebene <math>\epsilon</math><math>\rightarrow</math> trivial<br /> |
| Zeile 19: | Zeile 19: | ||
5)<math>A \notin\delta_2 </math>________________wegen nkomp(A,B,C,D)<br /> | 5)<math>A \notin\delta_2 </math>________________wegen nkomp(A,B,C,D)<br /> | ||
6)<math>A \in\delta_2 </math> und <math>B \in\epsilon </math>____________2) und 4)<br /> | 6)<math>A \in\delta_2 </math> und <math>B \in\epsilon </math>____________2) und 4)<br /> | ||
| − | 7)<math>\exists P</math> | + | 7)<math>\exists P</math>,<math>P \in\epsilon </math>,<math>A \in\delta_2 </math>________6) und Axiom I/6 |
| + | |||
| + | bleibt zu zeigen : <math>A\not\equiv P</math> | ||
Version vom 16. Dezember 2010, 15:45 Uhr
Beweisen Sie: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte.
Vor: Ebene 
Beh:  enthält weinigstens drei paarweise verschiedene Punkte
enthält weinigstens drei paarweise verschiedene Punkte
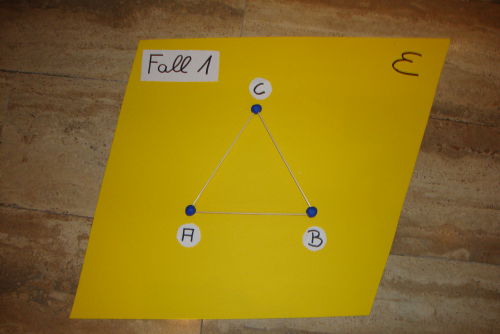
Fall 1:
3 der vier Punkte liegen in der Ebene 
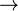 trivial
trivial
Fall 2:
2 der vier Punkte liegen in der Ebene 
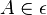 ,
,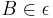
1) 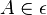 ,
, 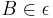 ,
, 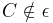 und
und 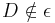
2)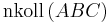
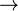
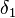 ________Lemma 3 und Axiom I/4
________Lemma 3 und Axiom I/4
3)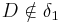 __________________wegen nkomp(A,B,C,D)
__________________wegen nkomp(A,B,C,D)
4)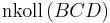
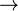
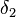 ___________3)
___________3)
5)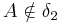 ________________wegen nkomp(A,B,C,D)
________________wegen nkomp(A,B,C,D)
6)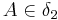 und
und 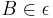 ____________2) und 4)
____________2) und 4)
7)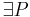 ,
,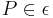 ,
,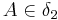 ________6) und Axiom I/6
________6) und Axiom I/6
bleibt zu zeigen :