Lösung von Aufg. 7.7 (SoSe 11)

Es seien 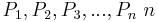$\ P_1, P_2, P_3, ..., P_n \ n$ verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser $n$ Punkte gehen? Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.

Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. Formulieren Sie obige Aufgabe für Schüler dieser Schulstufe.

Lösung:
i) Dadurch dass die je 3 Punkte nicht kolinear sind, geht es also darum die Anzahl der Punktepaare zu bestimmen, bei denen die Reihnfolge nicht beachtet wird (da AB=BA). Seien es n Punkte => P_1 bildet mit den restlichen P_i, n-1 Graden. Dann wählt man P_2 der bildet mit den restlichen Punkte P_i, i = 2,..,n, n-2 Graden usw. Die Summe dieser Anzahl von Graden ist die Gaußsche Summenformmel b: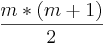$\frac{m * (m+1)}{2}$. Wobei hier m = n - 1 zu setzten ist.

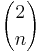
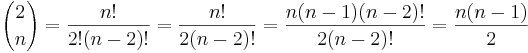
Einfacher ist es vielleicht über den Binomialkoeffizient da die Anzahl der Graden gleich der Anzahl der zweielementigen Teilmengen der Mengen der Punkte ist. ${2 \choose n}$ ${2 \choose n} = \frac{ n! }{ 2! (n-2) !} = \frac{ n! }{ 2 (n-2) !} = \frac{n (n-1) (n-2)!}{2(n-2)!} = \frac{n(n-1)}{2}$

ii) Für die 7te Klasste der Hauptschule wäre vielleicht eine adäquate Aufgabe die Zahlen von 1 bis 100 zu summieren und so auf die Formel geleitet zu werden. Dafür gibt es ja eine recht anschauliche Herleitung--Peterpummel 13:18, 23. Mai 2011 (CEST)