Lösung von Aufg. 8.2 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt g…“) |
|||
| Zeile 1: | Zeile 1: | ||
Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \Epsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält. | Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \Epsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält. | ||
| + | Vor: Gerade g, Punkt P, P <math></math> g | ||
| + | Beh: Ebene E: P <math>\in E und g ist Teilmenge von E | ||
| + | 1.)\exists A,B: A,B \in g [Axiom I.2] | ||
| + | 2.)\exists P: P \not\in g und nkoll (A,B,P) [Vor., Axiom I.3] | ||
| + | 3.)\exists E: P \in E und g ist Teilmenge von E</math><math>\in E und g ist Teilmenge von E</math> [1.), 2.), Axiom I.4] | ||
| + | |||
| + | qed. | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 1. Juni 2011, 11:37 Uhr
Es sei 
eine Gerade und 
ein Punkt, der nicht zu gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene 
, die sowohl alle Punkte von als auch den Punkt enthält.
Vor: Gerade g, Punkt P, P g
Beh: Ebene E: P ![\in E und g ist Teilmenge von E
1.)\exists A,B: A,B \in g [Axiom I.2]
2.)\exists P: P \not\in g und nkoll (A,B,P) [Vor., Axiom I.3]
3.)\exists E: P \in E und g ist Teilmenge von E](/images/math/6/4/3/6434f072711ea98cbbac221edb6604ca.png)
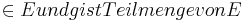[1.), 2.), Axiom I.4]
qed.
