Lösung von Aufgabe 10.3: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Beweis Versuch 1:<br /> Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten:<br /> Jede Stecke hat in jeder Ebenen, zu der die Strecke vollständig geh...)
 
(→‎Beweis Versuch 1:)
 
(5 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
[[Beweis Versuch 1:]]<br />
+
[[Mittelsenkrechte_und_Winkelhalbierende#Satz_VI.1:_.28Existenz_und_Eindeutigkeit_der_Mittelsenkrechten.29|Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten (in Formelschreibweise)]]
 +
 
 +
==Lösung--[[Benutzer:Schnirch|Schnirch]] 13:14, 21. Jul. 2010 (UTC)==
 +
Nach dem bereits bewiesenen Satz über die Existenz und Eindeutigkeit des Mittelpunkts, existiert zu jeder Strecke <math>\overline{AB}</math> genau ein Mittelpunkt <math>\ M </math>. Nach dem bereits bewiesenen Satz über die Existenz und Eindeutigkeit einer Senkrechten zu einer Geraden <math>\ g </math> durch einen beliebigen Punkt <math>\ P \in g </math> existiert genau eine Senkrechte auf eine Gerade <math>\ AB </math> durch den Mittelpunkt <math>\ M </math> der Strecke <math>\overline{AB} </math>. Diese existierende und eindeutige Senkrechte ist nach Definition die Mittelsenkrechte durch den Punkt <math>\ M </math> auf <math>\overline{AB} </math>.
 +
 
 +
==vorangegangene Diskussion==
 +
 
 +
== Beweis Versuch 1:==
 +
 
 
[[Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten:]]<br />
 
[[Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten:]]<br />
 
Jede Stecke hat in jeder Ebenen, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
 
Jede Stecke hat in jeder Ebenen, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
  
−
Als Voraussetzung ist die Strecke math> \overline{AB}</math>, die Ebene E zu benennen. <br />
+
Als Voraussetzung ist die Strecke <math> \overline{AB}</math>, die Ebene E zu benennen. <br />
−
Nun ist zu zeigen, dass es in <math>E</math>eine Gerade <math>m</math>gibt, die die Mittelsenkrechte zur Strecke math> \overline{AB}</math> ist. Und, dass es nicht mehr als diese eine gibt.<br />
+
Nun ist zu zeigen, dass es in <math>E</math> eine Gerade <math>m</math> gibt, die die Mittelsenkrechte zur Strecke <math> \overline{AB}</math> ist. Und, dass es nicht mehr als diese eine gibt.<br />
  
 
(1) Es gibt ein Punkt <math>Q</math>, der zur Ebene E gehört, aber nicht zur Geraden <math>AB</math>. <br />
 
(1) Es gibt ein Punkt <math>Q</math>, der zur Ebene E gehört, aber nicht zur Geraden <math>AB</math>. <br />
−
(2) Es existiert genau ein Mittelpunkt <math>M</math> auf der Strecke <math> \overline{AB}</math>, nach Existenz und Eindeutigkeit Mittelpunkt.
+
(2) Es existiert genau ein Mittelpunkt <math>M</math> auf der Strecke <math> \overline{AB}</math>, nach Existenz und Eindeutigkeit Mittelpunkt.<br />
 
(3) Es existiert ein Punkt <math>P</math>in der Halbebenen <math> AB,Q^{+} </math> und somit ein genau ein Strahl <math> MP^{+} </math>. Der Winkel <math> \angle PMB </math> hat das Maß 90, nach Winkelkonstruktionsaxiom.<br />
 
(3) Es existiert ein Punkt <math>P</math>in der Halbebenen <math> AB,Q^{+} </math> und somit ein genau ein Strahl <math> MP^{+} </math>. Der Winkel <math> \angle PMB </math> hat das Maß 90, nach Winkelkonstruktionsaxiom.<br />
 
(4) Die Gerade <math>PM</math> ist Mittelsenkrechte der Strecke <math> \overline{AB}</math>.<br />
 
(4) Die Gerade <math>PM</math> ist Mittelsenkrechte der Strecke <math> \overline{AB}</math>.<br />

Aktuelle Version vom 21. Juli 2010, 15:14 Uhr

Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten (in Formelschreibweise)

Lösung--Schnirch 13:14, 21. Jul. 2010 (UTC)

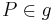Nach dem bereits bewiesenen Satz über die Existenz und Eindeutigkeit des Mittelpunkts, existiert zu jeder Strecke \overline{AB} genau ein Mittelpunkt \ M . Nach dem bereits bewiesenen Satz über die Existenz und Eindeutigkeit einer Senkrechten zu einer Geraden \ g durch einen beliebigen Punkt \ P \in g existiert genau eine Senkrechte auf eine Gerade \ AB durch den Mittelpunkt \ M der Strecke \overline{AB} . Diese existierende und eindeutige Senkrechte ist nach Definition die Mittelsenkrechte durch den Punkt \ M auf \overline{AB} .

vorangegangene Diskussion

Beweis Versuch 1:

Satz VI.1: Existenz und Eindeutigkeit der Mittelsenkrechten:
Jede Stecke hat in jeder Ebenen, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.

Als Voraussetzung ist die Strecke \overline{AB}, die Ebene E zu benennen.
Nun ist zu zeigen, dass es in E eine Gerade m gibt, die die Mittelsenkrechte zur Strecke \overline{AB} ist. Und, dass es nicht mehr als diese eine gibt.

(1) Es gibt ein Punkt Q, der zur Ebene E gehört, aber nicht zur Geraden AB.
(2) Es existiert genau ein Mittelpunkt M auf der Strecke \overline{AB}, nach Existenz und Eindeutigkeit Mittelpunkt.
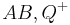(3) Es existiert ein Punkt Pin der Halbebenen AB,Q^{+} und somit ein genau ein Strahl 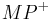MP^{+} . Der Winkel 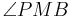\angle PMB hat das Maß 90, nach Winkelkonstruktionsaxiom.
(4) Die Gerade 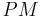PM ist Mittelsenkrechte der Strecke \overline{AB}.

Die Existenz und die Eindeutigkeit (wegen Winkelkonstruktionsaxiom) ist gezeigt.

qed --Löwenzahn 17:30, 1. Jul. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_10.3&oldid=3524“