Lösung von Aufgabe 5.6: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation <math>\ \Theta</math> (<math>\ \Theta</math> ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge <math>\ E \setminus g</math> (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige <math>\ A,B \in E \setminus g</math> gilt: <math>\ A \Theta B: \Leftrightarrow \overline{AB}\cap g = | + | Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation <math>\ \Theta</math> (<math>\ \Theta</math> ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge <math>\ E \setminus g</math> (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige <math>\ A,B \in E \setminus g</math> gilt: <math>\ A \Theta B: \Leftrightarrow \overline{AB}\cap g = \lbrace \rbrace</math>.<br /> |
a) Beschreiben Sie die Relation <math>\ \Theta</math> verbal und veranschaulichen Sie diese Relation.<br /> | a) Beschreiben Sie die Relation <math>\ \Theta</math> verbal und veranschaulichen Sie diese Relation.<br /> | ||
b) Begründen Sie anschaulich, dass <math>\ \Theta</math> eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation <math>\ \Theta</math> bezogen.<br /> | b) Begründen Sie anschaulich, dass <math>\ \Theta</math> eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation <math>\ \Theta</math> bezogen.<br /> | ||
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.<br /> | Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.<br /> | ||
| + | |||
| + | Ist hier ein Tippfehler drin oder soll es AB geschnitten mit g = 0 heißen? Wenn ja bedeutet das, dass es die leere Menge ist? Diese 0 verwirrt mich!!<br /> | ||
| + | Die 0 steht für die Leere Menge, ich habe es zum besseren Verständnis geändert in : <math>\lbrace \rbrace</math>, OK?--[[Benutzer:Schnirch|Schnirch]] 13:12, 15. Nov. 2010 (UTC)<br /> | ||
a) Die Punkte A und B stehen genau dann in Relation, wenn die Strecke AB keinen Schnittpunkt mit g hat.<br /> | a) Die Punkte A und B stehen genau dann in Relation, wenn die Strecke AB keinen Schnittpunkt mit g hat.<br /> | ||
Version vom 15. November 2010, 15:12 Uhr
Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation 
( ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge 
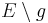(also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 
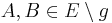gilt: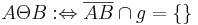 
.
a) Beschreiben Sie die Relation verbal und veranschaulichen Sie diese Relation.
b) Begründen Sie anschaulich, dass eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation bezogen.
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.
Ist hier ein Tippfehler drin oder soll es AB geschnitten mit g = 0 heißen? Wenn ja bedeutet das, dass es die leere Menge ist? Diese 0 verwirrt mich!!
Die 0 steht für die Leere Menge, ich habe es zum besseren Verständnis geändert in :, OK?--Schnirch 13:12, 15. Nov. 2010 (UTC)
a) Die Punkte A und B stehen genau dann in Relation, wenn die Strecke AB keinen Schnittpunkt mit g hat.
b) Reflexivität: aRa
zu zeigen: Strecke AA geschnitten mit g ist die leere Menge.
Bei der Strecke AA handelt es sich um einen Punkt. Laut Vorrausetzung liegt der Punkt in E, hat aber keinen Schnittpunkt mit g.
Somit gilt: Strecke AA geschnitten mit g ist die leere Menge.
Symmetrie: aRb, bRa
zu zeigen:
- Strecke AB geschnitten mit g ist die leere Menge,
- Strecke BA geschnitten mit g ist auch die leere Menge.
Bei den Strecken AB und BA handelt es sich um die gleiche Strecke. Nach Voraussetzung liegen die Punkte A und B in der Ebene haben aber keinen Schnittpunkt mit g. (Wenn die Strecke AB keinen Schnittpunkt mit g hat, dann hat auch die Strecke BA keinen Schnittpunkt mit g).
Es gilt:
- Strecke AB geschnitten mit g ist die leere Menge,
- Strecke BA geschnitten mit g ist auch die leere Menge.
Transitivität: aRb, bRc draus folgt aRc
Die Punkte A, B, C liegen in der Ebene und haben keinen Schnittpunkt mit g.
Schneidet g die Seiten AB und BC des Dreiecks ABC nicht, dann wird auch die Seite AC nicht von g geschnitten.- Satz von Pasch --Engel82 00:45, 11. Nov. 2010 (UTC)
