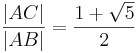Lösung von Aufgabe 7.3: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Der Punkt <math>\ B</math> möge die Strecke <math>\overline{AC}</math> derart in die Teilstrecken <math>\overline{AB}</math> und <math>\overline{BC}</math> teilen, das...)
 
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 1: Zeile 1:
 
Der Punkt <math>\ B</math> möge die Strecke <math>\overline{AC}</math> derart in die Teilstrecken <math>\overline{AB}</math> und <math>\overline{BC}</math> teilen, dass <math>\left| AB \right| > \left| BC \right|</math> gilt. Beweisen Sie:<br />
 
Der Punkt <math>\ B</math> möge die Strecke <math>\overline{AC}</math> derart in die Teilstrecken <math>\overline{AB}</math> und <math>\overline{BC}</math> teilen, dass <math>\left| AB \right| > \left| BC \right|</math> gilt. Beweisen Sie:<br />
 
Wenn <math>\frac{ \left| AC \right| }{\left| AB \right| } = \frac{\left| AB \right| }{\left| BC \right| }</math>, dann <math>\frac{ \left| AC \right| }{\left| AB \right|} = \frac{1 + \sqrt{5}}{2}</math>.
 
Wenn <math>\frac{ \left| AC \right| }{\left| AB \right| } = \frac{\left| AB \right| }{\left| BC \right| }</math>, dann <math>\frac{ \left| AC \right| }{\left| AB \right|} = \frac{1 + \sqrt{5}}{2}</math>.
 +
 +
<span style="color: blue">Die nachfolgende Lösung von Sternchen ist super ausführlich und korrekt, also wirklich eine Musterlösung - Großes LOB!!! --[[Benutzer:Schnirch|Schnirch]] 10:25, 1. Jul. 2010 (UTC)
 +
 +
</span>
 +
<u>Voraussetzung:</u>
 +
:1) <math>\frac{|AC|}{|AB|} = \frac{|AB|}{|BC|}</math>
 +
:2) <math>\ |AB| + |BC| = |AC|</math>
 +
<u>Behauptung:</u>
 +
:<math>\frac{|AC|}{|AB|} = \frac{1 + \sqrt{5}}{2}</math>
 +
<u>Beweis:</u>
 +
:(2) <math>\ |AB| + |BC| = |AC|</math>
 +
:<math>\Rightarrow \ \ |BC| = |AC| - |AB|</math>
 +
:eingesetzt in (1) folgt daraus
 +
:<math>\frac{|AC|}{|AB|} = \frac{|AB|}{|AC| - |AB|} \ \ \ \ \ | \ \cdot |AB| \cdot(|AC| - |AB|)</math>
 +
:<math>\Rightarrow \ \ |AC| \cdot (|AC| - |AB|) = |AB|^2 \ \ \ \ \ | \ -|AB|^2</math>
 +
:<math>\Rightarrow \ \ |AC|^2 - |AB| \cdot |AC| - |AB|^2 = 0</math>
 +
:Mit der p,q-Formel folgt daraus
 +
:<math>|AC|_{1/2} = \frac{|AB|}{2} \pm \sqrt{\frac{|AB|^2}{4} + |AB|^2}</math>
 +
:Die 2. Lösung mit negativem Vorzeichen fällt weg.
 +
:<math>\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \sqrt{ \frac{5 \cdot |AB|^2}{4} }</math>
 +
:<math>\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \frac{|AB|}{2} \cdot \sqrt{5}</math>
 +
:<math>\Rightarrow \ \ |AC| = \frac{|AB|}{2} \cdot ( 1 + \sqrt{5})</math>
 +
:<math>\Rightarrow \ \ |AC| = |AB| \cdot \frac{ 1 + \sqrt{5} }{2} \ \ \ \ \ | \ : |AB|</math>
 +
:<math>\Rightarrow \ \ \frac{|AC|}{|AB|} = \frac{ 1 + \sqrt{5} }{2}</math>
 +
:q.e.d --[[Benutzer:Sternchen|Sternchen]] 17:05, 10. Jun. 2010 (UTC)

Aktuelle Version vom 1. Juli 2010, 12:25 Uhr

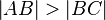Der Punkt \ B möge die Strecke \overline{AC} derart in die Teilstrecken \overline{AB} und \overline{BC} teilen, dass \left| AB \right| > \left| BC \right| gilt. Beweisen Sie:
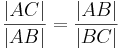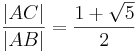Wenn \frac{ \left| AC \right| }{\left| AB \right| } = \frac{\left| AB \right| }{\left| BC \right| }, dann \frac{ \left| AC \right| }{\left| AB \right|} = \frac{1 + \sqrt{5}}{2}.

Die nachfolgende Lösung von Sternchen ist super ausführlich und korrekt, also wirklich eine Musterlösung - Großes LOB!!! --Schnirch 10:25, 1. Jul. 2010 (UTC)

Voraussetzung:

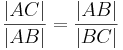
1) \frac{|AC|}{|AB|} = \frac{|AB|}{|BC|}
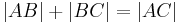
2) \ |AB| + |BC| = |AC|

Behauptung:

\frac{|AC|}{|AB|} = \frac{1 + \sqrt{5}}{2}

Beweis:

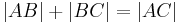
(2) \ |AB| + |BC| = |AC|
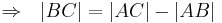
\Rightarrow \ \ |BC| = |AC| - |AB|
eingesetzt in (1) folgt daraus
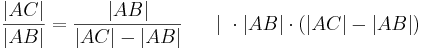
\frac{|AC|}{|AB|} = \frac{|AB|}{|AC| - |AB|} \ \ \ \ \ | \ \cdot |AB| \cdot(|AC| - |AB|)
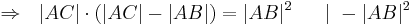
\Rightarrow \ \ |AC| \cdot (|AC| - |AB|) = |AB|^2 \ \ \ \ \ | \ -|AB|^2
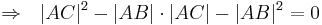
\Rightarrow \ \ |AC|^2 - |AB| \cdot |AC| - |AB|^2 = 0
Mit der p,q-Formel folgt daraus
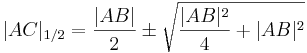
|AC|_{1/2} = \frac{|AB|}{2} \pm \sqrt{\frac{|AB|^2}{4} + |AB|^2}
Die 2. Lösung mit negativem Vorzeichen fällt weg.
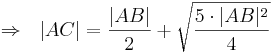
\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \sqrt{ \frac{5 \cdot |AB|^2}{4} }
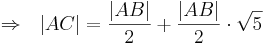
\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \frac{|AB|}{2} \cdot \sqrt{5}
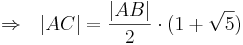
\Rightarrow \ \ |AC| = \frac{|AB|}{2} \cdot ( 1 + \sqrt{5})
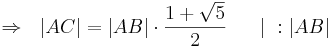
\Rightarrow \ \ |AC| = |AB| \cdot \frac{ 1 + \sqrt{5} }{2} \ \ \ \ \ | \ : |AB|
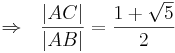
\Rightarrow \ \ \frac{|AC|}{|AB|} = \frac{ 1 + \sqrt{5} }{2}
q.e.d --Sternchen 17:05, 10. Jun. 2010 (UTC)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_7.3&oldid=2525“