Lösung von Aufgabe 7.4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Definieren noch einmal die Begriffe Halbgerade <math>\ AQ^{+}</math> und <math>\ AQ^{-}</math>. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht expl...) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Definieren noch einmal die Begriffe Halbgerade <math>\ AQ^{+}</math> und <math>\ AQ^{-}</math>. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur [http://wikis.zum.de/geowiki/index.php/Strecken#Definition_II.3:_.28Halbgerade.2C_bzw._Strahl.29 | Definition II.3] äquivalent sind. | Definieren noch einmal die Begriffe Halbgerade <math>\ AQ^{+}</math> und <math>\ AQ^{-}</math>. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur [http://wikis.zum.de/geowiki/index.php/Strecken#Definition_II.3:_.28Halbgerade.2C_bzw._Strahl.29 | Definition II.3] äquivalent sind. | ||
| + | |||
| + | == Lösung --[[Benutzer:Schnirch|Schnirch]] 13:27, 7. Jul. 2010 (UTC)== | ||
| + | 1a) <math>\ AQ^{+} = \{P \in AQ| A \not \in \overline{PQ}\} \cup \{A\} </math> <br\> | ||
| + | 2a) <math>\ AQ^{-} = \{P| A \in \overline{PQ} \} </math> | ||
| + | |||
| + | 1b) <math>AQ^+ := \{ P \mid \operatorname{Zw}(A,P,Q) \lor \operatorname{Zw}(A,Q,P) \} \cup \{ A,Q \}</math> <br\> | ||
| + | 2b) <math>AQ^-:=\left \{ P|Zw(P,A,Q)\right \}\cup \left \{A \right \}</math> | ||
| + | |||
| + | es ist die Mengengleichheit von 1a) und 1b) bzw. 2a) und 2b) zu zeigen. <br\> | ||
| + | Gezeigt werden kann dies, indem man zeigt, dass die in 1a) definierte Menge Teilmenge der in 1b) definierten Menge ist und die in 1b) definierte Menge Teilmenge der in 1a) definierten Menge ist. | ||
| + | |||
| + | |||
| + | {| class="wikitable " | ||
| + | |+ Beweis | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | <math>AQ^+ := \{ P \mid \operatorname{Zw}(A,P,Q) \lor \operatorname{Zw}(A,Q,P) \} \cup \{ A,Q \}</math> <br\> | ||
| + | | Voraussetzung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | <math>\{ P \mid \operatorname{Zw}(A,P,Q) \} \Rightarrow P \in AQ \and A \not \in \overline{PQ} </math> <br\> | ||
| + | | Def. Zw | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | <math>\{ P \mid \operatorname{Zw}(A,Q,P) \} \Rightarrow P \in AQ \and A \not \in \overline{PQ} </math> <br\> | ||
| + | | Def. Zw | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | zu betrachten ist noch: <math> \{ A,Q \} \in AQ^+ </math> <br\> Punkt A ist in beiden Mengen vorhanden <br\> | ||
| + | sowohl 1b) als auch 1a) schließt den Punkt <math> Q </math> mit ein. | ||
| + | | nach Definition der beiden Mengen <br\> nach Definition 1a) gilt: wenn <math> P = Q </math> dann: <math> A \not \in \overline{PQ} </math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | Menge aus Definition 1a) <math>\subseteq </math> Menge aus Definition 1b) | ||
| + | | (II), (III), (IV) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VI) | ||
| + | | <math>\ AQ^{+} = \{P \in AQ| A \not \in \overline{PQ}\} \cup \{A\} </math> | ||
| + | | Voraussetzung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VII) | ||
| + | | <math>\ koll(A,Q,P) </math> | ||
| + | | <math> P \in AQ </math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VIII) | ||
| + | | <math>\operatorname{Zw}(A,P,Q)\or \operatorname{Zw}(A,Q,P)</math> | ||
| + | | (VI), (VII), Definition Zw. | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IIX) | ||
| + | | Menge aus Definition 1b) <math>\subseteq </math> Menge aus Definition 1a) | ||
| + | | (IV), (VIII) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IX) | ||
| + | | Menge aus Definition 1b) = Menge aus Definition 1a) | ||
| + | | (V), (IIX) | ||
| + | |- | ||
| + | |} | ||
Aktuelle Version vom 7. Juli 2010, 15:27 Uhr
Definieren noch einmal die Begriffe Halbgerade 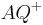 und
und 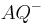 . In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.3 äquivalent sind.
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.3 äquivalent sind.
Lösung --Schnirch 13:27, 7. Jul. 2010 (UTC)
1a) 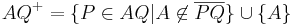
2a) 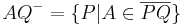
1b) 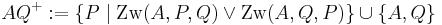
2b) 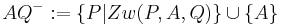
es ist die Mengengleichheit von 1a) und 1b) bzw. 2a) und 2b) zu zeigen.
Gezeigt werden kann dies, indem man zeigt, dass die in 1a) definierte Menge Teilmenge der in 1b) definierten Menge ist und die in 1b) definierte Menge Teilmenge der in 1a) definierten Menge ist.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 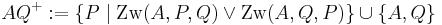 |
Voraussetzung |
| (II) | 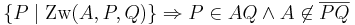 |
Def. Zw |
| (III) | 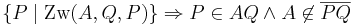 |
Def. Zw |
| (IV) | zu betrachten ist noch: 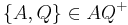 Punkt A ist in beiden Mengen vorhanden sowohl 1b) als auch 1a) schließt den Punkt |
nach Definition der beiden Mengen nach Definition 1a) gilt: wenn 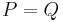 dann: dann: 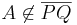
|
| (V) | Menge aus Definition 1a) 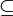 Menge aus Definition 1b) Menge aus Definition 1b)
|
(II), (III), (IV) |
| (VI) | 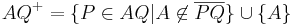
|
Voraussetzung |
| (VII) | 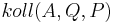
|
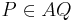
|
| (VIII) | 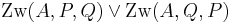
|
(VI), (VII), Definition Zw. |
| (IIX) | Menge aus Definition 1b) 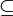 Menge aus Definition 1a) Menge aus Definition 1a)
|
(IV), (VIII) |
| (IX) | Menge aus Definition 1b) = Menge aus Definition 1a) | (V), (IIX) |
 mit ein.
mit ein.

