Lösung von Aufgabe 9.1P (SoSe 13)
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
- Schritt 4 und 5 sind z.B. noch nicht korrekt. Strecken lassen sich nicht addieren!--Tutorin Anne 21:45, 18. Jul. 2013 (CEST)
| Voraussetzung | 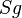 mit mit 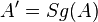 und und 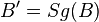 und und 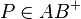
|
| Behauptung | 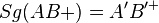 d.h. d.h. 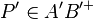
|
| Beweisschritt | Begründung |
|---|---|
1 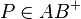 |
Voraussetzung |
2 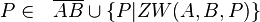 |
1), Def Halbgerade |
3 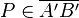 |
Streckentreue |
4 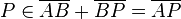 |
Def Zwischen |
5 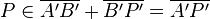 |
Abstandserhaltung der Geradenspiegelung |
6 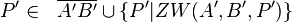 |
Def Zwischen 3), 5) |
7 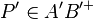 |
Def Halbgerade 6) |
--Regenschirm 17:50, 25. Jun. 2013 (CEST)
Die Beweisidee und Schritte sind super. Es fehlen noch ein paar Striche und Klammern, damit der Beweis auch ganz richtig ist.--Tutorin Anne 15:18, 26. Jun. 2013 (CEST)
- Darf man eigentlich
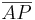 schreiben?
schreiben?  ist doch ein Vertreter aller Punkte innerhalb der Halbgerade Fehler beim Parsen(Syntaxfehler): \ AB^{+
ist doch ein Vertreter aller Punkte innerhalb der Halbgerade Fehler beim Parsen(Syntaxfehler): \ AB^{+
- Darf man eigentlich
und diese ist ja unendlich.--Nolessonlearned 14:08, 18. Jul. 2013 (CEST)
- Ja, das darf man. P ist ein beliebiger, aber in dem Moment wo ich ihn nenne ein fester Punkt. Und danach auch nicht mehr verschiebbar (d.h. ich kann nicht im nachhinein sagen, dass er eine bestimmte Eigenschaft erfüllt z.B. auf einer Mittelsenkrechten liegt. --Tutorin Anne 21:43, 18. Jul. 2013 (CEST)
Voraussetzung: 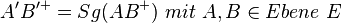
Definitionen gehören nicht in die Voraussetzung, sondern nur die "Mitspieler". Es ist sinnvoll sich die Definitionen am Rand zu notieren und in den Begründungsschritten dann Def. ... zu schreiben, wenn man sie verwendet hat. In seltenen Fällen v.a. dann wenn es mehrere Definitionen eines Begriffs gibt, kann man die Definition dann in der Begründung auch explizit nennen. --Tutorin Anne 11:47, 16. Jul. 2013 (CEST)
- Danke, habe die VSS geändert.--Nolessonlearned 21:01, 16. Jul. 2013 (CEST)
Behauptung: 
--Nolessonlearned 18:39, 14. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 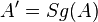
|
Eigenschaft Sg |
| 2) | 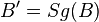
|
Eigenschaft Sg |
| 3) | 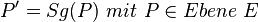
|
Eigenschaft Sg |
| 4) | 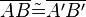
|
(1); (2); Voraussetzung; Streckentreue d. Sg |
| 5) | 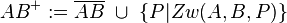
|
(1); (2); (3); Voraussetzung; Def. Halbgerade |
| 6) | 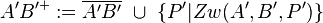
|
(4); (5); Voraussetzung; Def. Halbgerade; Eigenschaft Sg |
| 7) | 
|
(4); (5); (6)
q.e.d. |
--Nolessonlearned 18:57, 14. Jul. 2013 (CEST)
Schritt 6 kannst du nicht aus 4) und 5) herleiten, da eine Halbgerade ja noch aus weiteren Punkten besteht, die nicht auf der STrecke liegen. Diese könnten ja nicht aufeinander abgebildet werden. --Tutorin Anne 11:47, 16. Jul. 2013 (CEST)
- So könnte es passen.--Nolessonlearned 21:01, 16. Jul. 2013 (CEST)
- Du kannst die Zwischenrelation nicht einfach ersetzen. Du benötigst die Umformungsschitte, die auch im Beweis darüber zu finden sind. Nur dass da ein paar Fehler in der Schreibweise sind. --Tutorin Anne 09:52, 17. Jul. 2013 (CEST)

